|
 |
- Search
| Fire Sci. Eng. > Volume 33(5); 2019 > Article |
|
ņÜö ņĢĮ
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļ░öļŗźļ®┤ņØ┤ ņśżļ¬®ĒĢ£ ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ ļé┤ņŚÉ ņÜ®ņłś Ļ│ĄĻĖē ļģĖņ”ÉļĪ£ļČĆĒä░ ļéÖĒĢśĒĢ£ ņÜ®ņłśļĪ£ ņØĖĒĢ┤ ļ░£ņāØĒĢ£ ņłśļ®┤ņØś ņČ£ļĀüņ×äņØä ņłśņ╣ś ļ¬©ņØśĒĢśĻ│Ā ņĀĆņןĒā▒Ēü¼ņØś ņłśņ¦ü ļ▓Įļ®┤ņŚÉ ņ×æņÜ®ĒĢśļŖö ņ£Āņ▓┤ ļÅÖņłśļĀźņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ļ░ØĒśöļŗż. ļśÉĒĢ£ ĻĖ░ņĪ┤ņØś ņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢ£ ņłśņ╣ś ļ¬©ņØś ņŚ░ĻĄ¼ Ļ▓░Ļ│╝ņÖĆ ļ│Ė ņŚ░ĻĄ¼ņØś ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖļĪ£ ļÅÖņØ╝ĒĢ£ ņĪ░Ļ▒┤ņŚÉņä£ ņłśņ╣ś ļ¬©ņØś Ļ│äņé░ĒĢśņŚ¼ ņČ£ļĀüņ×äņØś ņĄ£ļīĆ ĒīīĻ│Ā ņśżļ”ä ļåÆņØ┤ņÖĆ ņČ£ļĀüņ×äņŚÉ ņØśĒĢ£ ļÅÖņłśļĀź ļ│ĆĒÖöļź╝ ņä£ļĪ£ ļ╣äĻĄÉĒĢśņśĆļŗż. ĻĘĖ Ļ▓░Ļ│╝, ņĀĆņןĒā▒Ēü¼ ļé┤ļČĆņŚÉ ļ░£ņāØĒĢśļŖö ņČ£ļĀüņ×äņØś ņøĆņ¦üņ×äĻ│╝ ņłśņ¦ü ļ▓Įļ®┤ņŚÉ ļ»Ėņ╣śļŖö ļÅÖņłśļĀźņØś ņśüĒ¢źņØä Ļ│ĀļĀżĒĢĀ ņłś ņ׳ĻĖ░ ņ£äĒĢ┤ņä£ļŖö ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņé¼ņÜ®ĒĢśļŖö Ļ▓āņØ┤ ļŹö ņĀüĒĢ®ĒĢśĻ▓ī ļ¬©ņØśļÉśļŖö Ļ▓āņØä ļ░ØĒśöļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ▓░Ļ│╝ļŖö ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ņØś ņĢłņĀĢņĀüņØĖ ĻĄ¼ņĪ░ ņäżĻ│äņŚÉ ĻĖ░ņŚ¼ĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ĻĖ░ļīĆĒĢ£ļŗż.
ABSTRACT
In the present study, the hydrodynamic force affected by a lapping wave induced by supplied falling water acting on the vertical wall of a portable water storage tank was analyzed using a nonlinear Peregrine model. The lapping waveŌĆÖs maximum run-up amplitudes and the hydrodynamic forces in the wall of the tank measured by linear and nonlinear PeregrineŌĆÖs models were compared numerically. As a result, it was concluded that the linear model may underestimate the effects on the vertical wall; therefore, it is more appropriate to use a nonlinear Peregrine model. Furthermore, this result can contribute to the stable structural designs of portable water storage tanks.
ļīĆĒśĢ ņé░ļČłĻ│╝ Ļ░ÖņØĆ ĒÖöņ×¼ĒśäņןņŚÉņä£ ņåīļ░®ņÜ®ņłśņØś ņøÉĒÖ£ĒĢ£ Ļ│ĄĻĖēņØä ņ£äĒĢ┤ ņ£Āļ¤Į, ļ»ĖĻĄŁ ļō▒ņŚÉņä£ļŖö ņåīļ░®ņÜ®ņłśļź╝ ņĀĆņןĒĢĀ ņłś ņ׳ļŖö ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼Ļ░Ć ņé¼ņÜ®ļÉśĻ│Ā ņ׳ņ£╝ļ®░, ĻĄŁļé┤ņŚÉņä£ļÅä ĻĄŁĻ░ĆņŚ░ĻĄ¼Ļ│╝ņĀ£ļź╝ ĒåĄĒĢśņŚ¼ ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼Ļ░Ć Ļ░£ļ░£ļÉśņŚłļŗż. Ļ░£ļ░£ļÉ£ ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ņŚÉ ņåīļ░®ņÜ®ņłśļź╝ Ļ│ĄĻĖēĒĢĀ ļĢī ņÜ®ņłś ļéÖĒĢśņŚÉ ņØśĒĢ┤ ļ░£ņāØĒĢśļŖö ņłśļ®┤ņØś ņČ£ļĀüņ×äņ£╝ļĪ£ ņØĖĒĢ£ ļÅÖņłśļĀź(Hydrodynamic force)ņØś ļ│ĆĒÖöĻ░Ć ņĀĆņןĒā▒Ēü¼ņØś ņłśņ¦üļ▓Įļ®┤ņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņŚÉ ļīĆĒĢ£ ĒĢ┤ņäØņØä ĒåĄĒĢśņŚ¼ ņĢłņĀäņä▒ņØä ĒÖĢņØĖĒĢśņśĆļŗż[1-3].
ļ©╝ņĀĆ Park ļō▒[1]ņØĆ ĒÅēĒÅēĒĢ£ ļ░öļŗźļ®┤ņØś ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ļź╝ ņ▓śņØīņ£╝ļĪ£ ļ¬©ļŹĖļ¦üĒĢśĻ│Ā ņåīļ░®ņÜ®ņłśņØś ļéÖĒĢśļĪ£ ņØĖĒĢśņŚ¼ ļ░£ņāØĒĢ£ ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×äņ£╝ļĪ£ ļ│ĆĒÖöļÉ£ ļÅÖņłśļĀź(Hydrodynamic force)ņØ┤ Ēā▒Ēü¼ņØś ņłśņ¦üļ▓Įļ®┤ņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ļČäņäØĒĢśņśĆļŗż. ņØ┤ ņŚ░ĻĄ¼ļŖö ņ×Éņ£Āņłśļ®┤ņØś ņČ£ļĀüņ×äņØä Boussinesq ļ░®ņĀĢņŗØņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļ¬©ļŹĖļ¦üĒĢśĻ│Ā ņłśņ╣ś ļ¬©ņØśļź╝ ĒåĄĒĢ┤ ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ņØś ļÅÖņłśļĀźņØä Ļ│äņé░ĒĢśņśĆļŗż. ļśÉĒĢ£ Park ļō▒[2]ņØĆ ņäĀĒśĢ Peregrine ļ░®ņĀĢņŗØņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņśżļ¬®ĒĢ£ ļ░öļŗźļ®┤ņØä Ļ░Ćņ¦ä ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ņØś ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ ļÅÖņłśļĀźņØä Ļ│äņé░ĒĢśņśĆļŗż. ņØ┤ ņŚ░ĻĄ¼ļź╝ ĒåĄĒĢ┤ ņĀĆņן Ēā▒Ēü¼ņØś ļ░öļŗźņØ┤ ņśżļ¬®ĒĢĀ Ļ▓ĮņÜ░ ņÜ®ņłś Ļ│ĄĻĖēņŚÉ ļö░ļźĖ ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×äņŚÉ ņØśĒĢ£ Ēā▒Ēü¼ ņłśņ¦üļ▓Įļ®┤ņŚÉ ļ»Ėņ╣śļŖö ļÅÖņłśļĀź ņ”ØĒÅŁņØ┤ ĻĄ¼ņĪ░ņĀü ņĢłņĀäņä▒ņŚÉ ņĢģņśüĒ¢źņØä ļ»Ėņ╣Ā ņłś ņ׳ņØīņØä ĒÖĢņØĖĒĢśņśĆļŗż. ņØ┤ņŚÉ ļö░ļØ╝ So ļō▒[3]ņØĆ ņĀĆņן Ēā▒Ēü¼ņØś ļ░öļŗźļ®┤ņØä ļ│╝ļĪØĒĢśĻ▓ī ņäżĻ│äĒĢśņŚ¼ ņłśņ¦ü ļ▓Įļ®┤ņ£╝ļĪ£ ņĀäĒīīļÉśļŖö ņČ£ļĀüņ×äņØä ļČäņé░ņŗ£Ēé┤ņ£╝ļĪ£ņŹ© ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ ļÅÖņłśļĀźņØś Ļ░ÉņåīļÉĀ ņłś ņ׳ļŖö Ļ▓āņØä ņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņé¼ņÜ®ĒĢ£ ņłśņ╣ś ļ¬©ņØśļĪ£ ļ░ØĒśöļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ĻĖ░ņĪ┤ Park ļō▒[2]ņŚÉņä£ ņé¼ņÜ®ĒĢ£ ņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ĒÖĢņןĒĢśņŚ¼ ļ╣äņäĀĒśĢ Peregrine ļ░®ņĀĢņŗØņØä ļÅäņ×ģĒĢśņŚ¼ ņÜ®ņłś ļéÖĒĢśļĪ£ ļ░£ņāØĒĢśļŖö ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×ä ņøĆņ¦üņ×äņØä ļ│┤ļŗż ĒśäņŗżņĀüņ£╝ļĪ£ ļ¬©ņØśĒĢśĻ│Ā Ēā▒Ēü¼ ņłśņ¦ü ļ▓Įļ®┤ņŚÉ ļ»Ėņ╣śļŖö ļÅÖņłśļĀź ļ│ĆĒÖöļź╝ ņłśņ╣ś ļ¬©ņØś ĒĢśņśĆļŗż. ņŚ░ĻĄ¼ Ļ▓░Ļ│╝ļŖö ņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļÅÖņØ╝ĒĢ£ ņłśņ╣ś ļ¬©ņØś ņĪ░Ļ▒┤ņ£╝ļĪ£ ņłśĒ¢ēĒĢ£ Ļ▓░Ļ│╝ņÖĆ ļ╣äĻĄÉ ļČäņäØĒĢśņŚ¼ Ēā▒Ēü¼ ļ▓Įļ®┤ņŚÉ ļ»Ėņ╣śļŖö ņČ£ļĀüņ×äņØś ņĄ£ļīĆ ņśżļ”ä ļåÆņØ┤ņÖĆ ļÅÖņłśļĀź ļ│ĆĒÖöĻ░Ć ņ¢┤ļ¢ĀĒĢ£ ņ░©ņØ┤ļź╝ Ļ░Ćņ¦ĆļŖöņ¦Ć ĒÖĢņØĖĒĢśĻ│Āņ×É ĒĢśņśĆļŗż. ļö░ļØ╝ņä£ ļ│Ė ņŚ░ĻĄ¼ļŖö ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×äņØä ņóĆ ļŹö ņŗżņĀ£ ņČ£ļĀüņ×äņØś ņøĆņ¦üņ×äņŚÉ ļ¦×Ļ▓ī ņłśņ╣ś ļ¬©ņØśĒĢĀ ņłś ņ׳Ļ│Ā ņØ┤ļŖö Ļ│¦ ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ņØś Ļ│╝ņåīĒÅēĻ░Ć ļÉśņ¦Ć ņĢŖņØĆ ļ│┤ļŗż ņĀĢļ░ĆĒĢ£ ļÅÖņłśļĀźņØä Ļ│äņé░ĒĢĀ ņłś ņ׳ņØīņØä ļ│┤ņØ┤Ļ│Āņ×É ĒĢśņśĆļŗż. ĻĘĖ Ļ▓░Ļ│╝ ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ņØś ļÅÖņłśļĀźņ£╝ļĪ£ ņØĖĒĢ£ ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ņØś ĻĄ¼ņĪ░ņĀü ņĢłņĀĢņä▒ņØä Ļ│ĀļĀżĒĢĀ ņłś ņ׳ļŖö ĻĘ╝Ļ▒░ļź╝ ļ¦łļĀ©ĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ĻĖ░ļīĆĒĢ£ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Ļ░ĆņÜ┤ļŹ░ ļ░öļŗźļ®┤ņØ┤ ņśżļ¬®ĒĢśņŚ¼ ņłśņ¦ü ļ▓Įļ®┤ņ£╝ļĪ£ ņśżļ”ä Ļ▓Įņé¼ļź╝ Ļ░Ćņ¦ä ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ ļé┤ņŚÉņä£ ņ×Éņ£Āņłśļ®┤ņØś ņČ£ļĀüņ×äņØä ņłśņ╣ś ļ¬©ņØśĒĢśĻĖ░ ņ£äĒĢ┤ ņןņŻ╝ĻĖ░ Ēīīļ×æ(ņČ£ļĀüņ×ä)ņØś ĒĢ┤ņäØņŚÉ ņé¼ņÜ®ļÉśļŖö ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖ[4,5]ņØä ļÅäņ×ģĒĢ£ļŗż.
ņŗØ(1)Ļ│╝ ņŗØ(2)ņØś ĒīīĻ│ĀĒĢ©ņłś(╬Ę)ņÖĆ ņłśņŗ¼ ĒÅēĻĘĀ(depth-averaged)ņØś ņ£ĀņåŹĒĢ©ņłś(u)Ļ░Ć ņŚ░ņä▒ļÉ£ ĒśĢĒā£ļĪ£ h(x)ļŖö Ēā▒Ēü¼ ļ░öļŗźĻ│╝ ņĀĢņ¦Ć ņłśļ®┤Ļ╣īņ¦ĆņØś ņłśņŗ¼ ĒĢ©ņłś, gļŖö ņżæļĀźĻ░ĆņåŹļÅä(=9.81 m/s2), ņĢäļלņ▓©ņ×ÉļŖö Ļ░üĻ░ü Ļ│ĄĻ░ä ļ░Å ņŗ£Ļ░ä ĒÄĖļ»ĖļČäņØä ļéśĒāĆļéĖļŗż. ļ╣äņäĀĒśĢ Peregrine ļ░®ņĀĢņŗØņØĆ ņäĀĒśĢ Peregrine ļ░®ņĀĢņŗØņŚÉ ļ╣äĒĢ┤ ņŗØ(2)ņØś ļ¬©ļ®śĒģĆ ĒĢŁņŚÉņä£ ļ╣äņäĀĒśĢ ĒĢŁ uuxņØ┤ ļŹö ņČöĻ░ĆļÉ£ ĒśĢĒā£ņØ┤ļ®░, ņŗØ(1)Ļ│╝ ņŗØ(2)ņØś ņ┤łĻĖ░ ņĪ░Ļ▒┤ņØĆ ļŗżņØīĻ│╝ Ļ░Öļŗż.
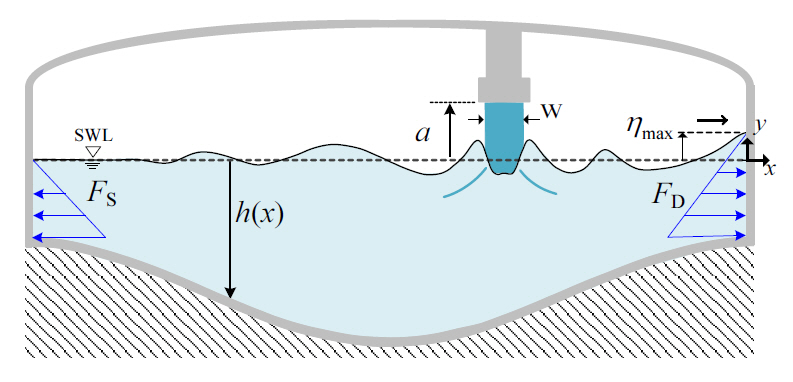
Figure 1ņØĆ ļéÖĒĢś ņÜ®ņłśņØś ĒśĢņāüņØä ņé¼Ļ░üĒśĢņØś ĒśĢĒā£ļĪ£ Ļ░ĆņĀĢĒĢśĻ│Ā ļ░öļŗźļ®┤ņØś ņśżļ¬®ĒĢ£ ņĀĆņן Ēā▒Ēü¼ņØś ĒśĢņāüĻ│╝ ņÜ®ņłś Ļ│ĄĻĖē ļģĖņ”ÉļĪ£ļČĆĒä░ ļéÖĒĢśĒĢśļŖö ņÜ®ņłśņŚÉ ņØśĒĢ┤ ļ░£ņāØĒĢ£ ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×äņØä Ļ░äļץĒ׳ ļéśĒāĆļéĖļŗż. aļŖö ņÜ®ņłś Ļ│ĄĻĖē ļģĖņ”ÉņØś ļåÆņØ┤, h(x)ļŖö ņĀĢņ¦Ć ņłśļ®┤ņŚÉņä£ ļ░öļŗźĻ╣īņ¦ĆņØś ņłśņŗ¼, ╬ĘmaxļŖö ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ņØś ņĄ£ļīĆ ĒīīĻ│Ā ņśżļ”ä ļåÆņØ┤, FSļŖö ņĀĢņ¦Ć ņłśļ®┤ņŚÉņä£ņØś ņ£Āņ▓┤ ņĀĢņłśļĀź, FDļŖö ╬ĘmaxņŚÉņä£ņØś ņ£Āņ▓┤ ļÅÖņłśļĀźņØä ļéśĒāĆļéĖļŗż. ņØ┤ļ¤¼ĒĢ£ ņŗ£ņŖżĒģ£ņØä ņłśņ╣ś Ļ│äņé░ĒĢśĻĖ░ ņ£äĒĢ┤ Jang [5]ņØś ĒĢ©ņłś ļ░śļ│Ą ĒĢ┤ļ▓ĢņØä ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ļÅäņ×ģĒĢ£ļŗż.
ņØ┤ļĢī, ņŗØ(4)ņŚÉņä£ XļŖö ļ▓ĪĒä░ ļ│ĆņłśņØ┤ļ®░,
ļ╣äņäĀĒśĢ ņŚ░ņé░ņ×É Th0ļŖö ļŗżņØīĻ│╝ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ ņŗØ(7)ņØś Y(j), j=1,2,3,4ļŖö Ļ░üĻ░ü ņĢäļלņÖĆ Ļ░ÖņØ┤ ņŚ░ņä▒ ņĀüļČäļ░®ņĀĢņŗØņØś ĒśĢĒā£ļĪ£ Ēæ£ĒśäļÉ£ļŗż.
ļśÉĒĢ£ ņŗØ(8)ņØś U(j), j=1,2,3,4ļŖö Ļ░üĻ░ü ļŗżņØīĻ│╝ Ļ░Öļŗż.
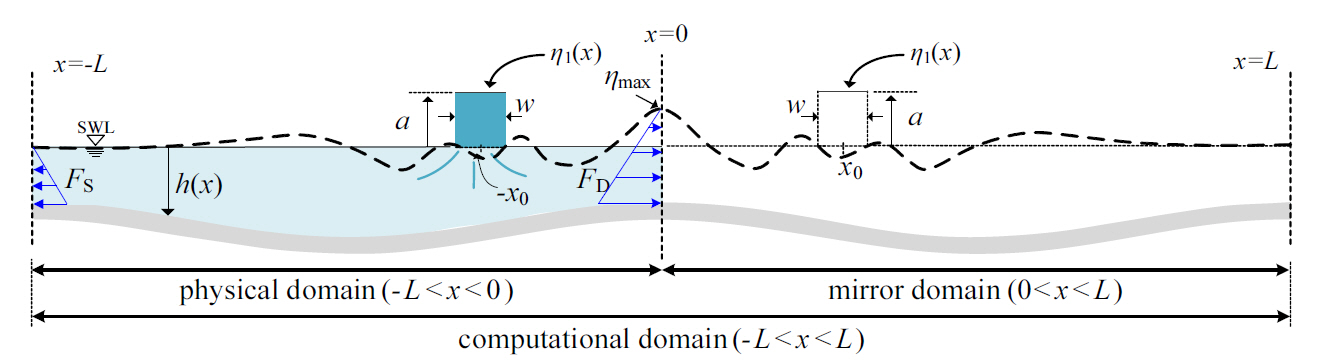
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ņØś ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×äņØ┤ ņĀäĒīīļÉśņ¢┤ ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ ņČ®ļÅīĒĢśļŖö Ļ▓āĻ│╝ ļÅÖņØ╝ĒĢ£ ņ×æņÜ®ņØä ņ£äĒĢ┤ Ļ▓Įņāü ņØ┤ļ»Ėņ¦Ć ļ¬©ļŹĖ[1-3,5]ņØä ļÅäņ×ģĒĢśņśĆĻ│Ā, ņØ┤ ļ¬©ļŹĖņØś ņłśņ╣ś Ļ│äņé░ ņśüņŚŁņØĆ Figure 2ņÖĆ Ļ░Öļŗż. ņØ┤ļĢī, ņĀĢņ¦Ć ņłśļ®┤ņŚÉņä£ ļģĖņ”ÉņØś ņ£äņ╣ś x = ┬▒x0ņŚÉņä£ ĒÅŁņØ┤ wņØ┤Ļ│Ā ļåÆņØ┤ aņŚÉņä£ ļéÖĒĢśĒĢśļŖö ņÜ®ņłś ╬Ę1(x) (ņŗØ(11))ņŚÉ ņØśĒĢ┤ ņ×Éņ£Āņłśļ®┤ņØś ņČ£ļĀüņ×äņØ┤ ļ░£ņāØĒĢ£ļŗż. ļ░śļ®┤ ņ┤łĻĖ░ ņ×Éņ£Ā ņłśļ®┤ņØĆ ņĀĢņ¦Ć ņāüĒā£(u1)ņØ┤ļŗż.
ņØ┤ļĢī ņśżļ¬®ĒĢ£ ļ░öļŗźļ®┤ņØä Ļ░ĆņĀĖ ņżæņĢÖņ£╝ļĪ£ļČĆĒä░ ņłśņ¦ü ļ▓Įļ®┤ņ£╝ļĪ£ Ļ▓Įņé¼ņ¦ä ļ░öļŗźļ®┤ņØś Ļ▓ĮņÜ░ļź╝ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ļ¬©ļŹĖļ¦ü ĒĢśņśĆļŗż.
ļ│Ė ņłśņ╣ś ļ¬©ņØśņŚÉņä£ Ļ│äņé░ņśüņŚŁņØĆ -20 m < x < 20 m (Ļ│ĄĻ░äĻ░äĻ▓® 0.1 m), ņŗ£Ļ░äņśüņŚŁņØä [0.2 s](ņŗ£Ļ░ä Ļ░äĻ▓® 0.5 s)ņ£╝ļĪ£ ņäżĻ│äĒĢśņśĆĻ│Ā, ļģĖņ”ÉņØś ĒÅŁņØä 0.8 mļĪ£ Ļ│ĀņĀĢĒĢśĻ│Ā ļģĖņ”ÉņØś ņ£äņ╣ś x0ņÖĆ ļģĖņ”ÉņØś ļåÆņØ┤ aļź╝ ļ│ĆĒÖöņŗ£Ēéżļ®┤ņä£ ņłśņ╣ś Ļ│äņé░ņØä ņłśĒ¢ēĒĢśņśĆļŗż. ĻĘĖļ”¼Ļ│Ā ļ¬©ņĪ░ ņāüņłś h0ļŖö ĒÅēĻĘĀ ņłśņŗ¼ņØĖ 0.8 mļĪ£ ĒĢśņśĆļŗż.
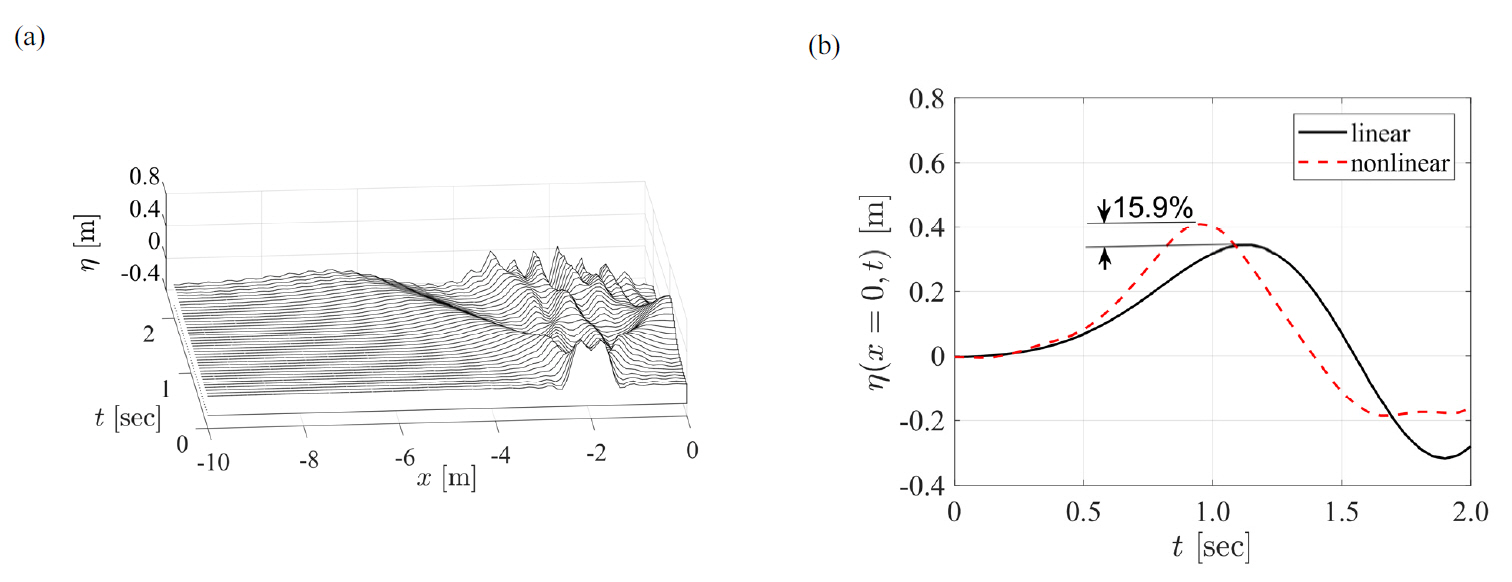
Figure 3(a)ņØĆ x0 = -2 mņØś ņ£äņ╣śņŚÉņä£ ļåÆņØ┤ a = 0.5 mņØś Ēü¼ĻĖ░ļĪ£ ļéÖĒĢśĒĢ£ ņÜ®ņłśļĪ£ ņØĖĒĢ┤ ļ░£ņāØĒĢ£ ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×äņØä ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņłśņ╣ś ļ¬©ņØśĒĢśņŚ¼ Ēā▒Ēü¼ ļé┤ ņČ£ļĀüņ×äņØä ļ¬©ņØśĒĢ£ Ļ▓░Ļ│╝ņØ┤ļŗż. ļśÉĒĢ£ Figure 3(b)ļŖö Figure 3(a)ņØś ņłśņ¦ü ļ▓Įļ®┤(x = 0)ņŚÉņä£ņØś ņŗ£Ļ│äņŚ┤ ņśżļ”ä ļåÆņØ┤(╬Ę(x = 0, t))ņÖĆ ņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņĀüņÜ®ĒĢśņŚ¼ ņ¢╗ņØĆ ņłśņ╣ś ļ¬©ņØśĒĢ£ Ēā▒Ēü¼ ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ņØś ņĄ£ļīĆ ĒīīĻ│Ā ņśżļ”ä ļåÆņØ┤ļź╝ ņä£ļĪ£ ļ╣äĻĄÉĒĢ£ Ļ▓āņØ┤ļŗż. Table 1ņŚÉņä£ Ļ│╝ņåī ņĀĢļÅä ĒÅēĻ░ĆņŗØ(13)ņŚÉ ļö░ļØ╝ Ļ│äņé░ĒĢ£ Ļ▓░Ļ│╝ļź╝ ļ│┤ļ®┤, ņäĀĒśĢ Peregrine ļ¬©ļŹĖņØś ļ¬©ņØśļŖö ļ╣äņäĀĒśĢ ņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņé¼ņÜ®ĒĢśņŚ¼ ņłśņ╣ś ļ¬©ņØśĒĢ£ ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×äņØ┤ Ēā▒Ēü¼ ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ņØś ņĄ£ļīĆ ņśżļ”ä ļåÆņØ┤ņØś Ļ▓░Ļ│╝ņŚÉ ļ╣äĒĢ┤ 6.8%~18.3% ņĀĢļÅä Ļ│╝ņåīĒÅēĻ░ĆļÉśņŚłņØīņØä ņĢī ņłś ņ׳ļŗż. ļśÉĒĢ£ Figure 3(b)ņÖĆ Ļ░ÖņØ┤ ĒīīĻ│ĀņØś ņ£äņāüņŚÉ ļīĆĒĢ┤ņä£ļÅä ņśżņ░©Ļ░Ć ļ░£ņāØļÉĀ ņłś ņ׳ņØīņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż.
ņäĀĒśĢ Peregrine ļ¬©ļŹĖĻ│╝ ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä Ļ░üĻ░ü ņé¼ņÜ®ĒĢśņŚ¼ ņÜ®ņłś Ļ│ĄĻĖē ļģĖņ”ÉņØś ņ£äņ╣ś x0(= -2 m, -3 m)ņÖĆ ļģĖņ”ÉļĪ£ļČĆĒä░ņØś ņÜ®ņłś ļéÖĒĢś ļåÆņØ┤ a(=0.2 m ~ 0.5 m)ņŚÉ ļö░ļźĖ ņłśņ¦ü ļ▓Įļ®┤(h(x = 0))ņŚÉņä£ņØś ņĄ£ļīĆ ĒīīĻ│Ā ņśżļ”ä ļåÆņØ┤ ╬Ęmaxļź╝ Ļ░üĻ░ü ļéśĒāĆļāłņŚłĻ│Ā, ņŗØ(14)ņŚÉ ņØśĒĢ£ ņĀĢņłśļĀź(FS)Ļ│╝ ļÅÖņłśļĀź(FD)ņØś ļ╣ä, Rļź╝ Table 1ņŚÉ ļéśĒāĆļé┤ņŚłļŗż[1-3].
Table 1ņØś Ļ▓░Ļ│╝ļĪ£ļČĆĒä░ ņäĀĒśĢ Peregrine ļ¬©ļŹĖņØś RLņØ┤ ļ╣äņäĀĒśĢ ļ¬©ļŹĖņØś RNLņÖĆ ļ╣äĻĄÉĒĢśņŚ¼ 2.6%Ōł╝13.0% ņĀĢļÅä (=|RL-RNL/RNL├Ś100%|)ņØś ļÅÖņłśļĀźņØä Ļ│╝ņåīĒÅēĻ░ĆĒĢśĻ│Ā ņ׳ļŖö Ļ▓āņ£╝ļĪ£ ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Ļ░ĆņÜ┤ļŹ░ ļ░öļŗźļ®┤ņØ┤ ņśżļ¬®ĒĢ£ ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ ļé┤ņŚÉ ņÜ®ņłś Ļ│ĄĻĖēņØä ņ£äĒĢśņŚ¼ ņÜ®ņłśļź╝ ļéÖĒĢśņŗ£Ēé¼ Ļ▓ĮņÜ░ ļ░£ņāØĒĢśļŖö ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×äņØä ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņłśņ╣ś ļ¬©ņØśļź╝ ņłśĒ¢ēĒĢśņśĆļŗż. ņØ┤ļź╝ ļ░öĒāĢņ£╝ļĪ£ ņĀĆņןĒā▒Ēü¼ ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ņØś ņČ£ļĀüņ×äņŚÉ ņØśĒĢ£ ĒīīĻ│ĀņØś ņĄ£ļīĆ ņśżļ”ä ļåÆņØ┤ļź╝ ņĖĪņĀĢĒĢśĻ│Ā ņłśņ¦ü ļ▓Įļ®┤ņŚÉ ļ»Ėņ╣śļŖö ļÅÖņłśļĀźņØś ļ│ĆĒÖöļ¤ēņØä Ļ│äņé░ĒĢśņŚ¼ ĻĘĖ ņśüĒ¢źņØä ĒÖĢņØĖĒĢśņśĆļŗż. ĻĘĖ Ļ▓░Ļ│╝ ļŗżņØīĻ│╝ Ļ░ÖņØĆ Ļ▓░ļĪĀņØä ņ¢╗ņŚłļŗż.
1) ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ļź╝ Ļ▓Įņāü ņØ┤ļ»Ėņ¦Ć ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņłśņ╣ś Ļ│äņé░ņśüņŚŁņØä ņäżņĀĢĒĢśņśĆņ£╝ļ®░, ņÜ®ņłś Ļ│ĄĻĖē ļģĖņ”ÉņØś ņ£äņ╣śņÖĆ ļģĖņ”ÉņØś ļåÆņØ┤(ņÜ®ņłś ļéÖĒĢś ļåÆņØ┤)ļź╝ ļ│ĆĒÖö ņŗ£Ēéżļ®┤ņä£ ļŗżņ¢æĒĢ£ ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×äņØä ņłśņ╣ś ļ¬©ņØśĒĢśņśĆļŗż.
2) ņ×Éņ£Ā ņłśļ®┤ņØś ņČ£ļĀüņ×äņØä ļ¬©ņØśĒĢśĻĖ░ ņ£äĒĢ┤ ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖņØś ņłśņ╣śņĀü ĒĢ┤ļ▓ĢņØä ļÅäņ×ģĒĢśņŚ¼ ņłśņ╣ś ļ¬©ņØśĒĢśĻ│Ā, ņÜ®ņłś ļéÖĒĢśņŚÉ ņØśĒĢ┤ ļ░£ņāØĒĢ£ ņČ£ļĀüņ×äņØś Ēā▒Ēü¼ ņłśņ¦ü ļ▓Įļ®┤ņŚÉņä£ņØś ņĄ£ļīĆ ņśżļ”ä ļåÆņØ┤ņÖĆ ļÅÖņłśļĀźņØä Ļ│äņé░ĒĢśņśĆņ£╝ļ®░, ĻĘĖ Ļ▓░Ļ│╝ļź╝ ņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņ¢╗ņØĆ ņłśņ╣ś ļ¬©ņØś Ļ▓░Ļ│╝ļź╝ ĒåĄĒĢ┤ ņ¢╗ņØĆ ņČ£ļĀüņ×äņØś ņĄ£ļīĆ ņśżļ”ä ļåÆņØ┤ ļ░Å ļÅÖņłśļĀźņØś Ļ▓░Ļ│╝ņÖĆ ņä£ļĪ£ ļ╣äĻĄÉĒĢśņśĆļŗż.
3) ĻĘĖ Ļ▓░Ļ│╝, ņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņé¼ņÜ®ĒĢ£ Ļ▓ĮņÜ░Ļ░Ć ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņé¼ņÜ®ĒĢśņŚ¼ ņłśņ╣ś ļ¬©ņØśĒĢśņśĆņØä Ļ▓ĮņÜ░ņŚÉ ļ╣äĒĢ┤ ņĄ£ļīĆ ĒīīĻ│Ā ņśżļ”ä ļåÆņØ┤ņÖĆ ĻĘĖņŚÉ ļö░ļźĖ ļÅÖņłśļĀźņØä Ļ│╝ņåīĒÅēĻ░ĆļÉĀ ņłś ņ׳ņØīņØä ĒÖĢņØĖĒĢśņśĆļŗż.
ļö░ļØ╝ņä£ ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ ļé┤ņØś ņÜ®ņłś ļéÖĒĢśņŚÉ ņØśĒĢ£ ņČ£ļĀüņ×äņØä ņłśņ╣ś ļ¬©ņØśĒĢśļŖöļŹ░ ņ׳ņ¢┤ņä£ļŖö ļ╣äņäĀĒśĢ Peregrine ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśļŖö Ļ▓āņØ┤ ņŗżņĀ£ ņČ£ļĀüņ×äņŚÉ ņØśĒĢ£ ļÅÖņłśļĀźĻ│╝ņØś ņśżņ░©ļź╝ ņżäņØ╝ ņłś ņ׳ļŗż. ļśÉĒĢ£ ļÅÖņłśļĀź ņé░ņĀĢņŚÉņä£ ņśżņ░©ļź╝ ņżäņØ╝ ņłś ņ׳ņØĆ Ļ▓āņØĆ ņĀĆņןĒā▒Ēü¼ņØś ļ▓Įļ®┤ņØä ņ¦ĆĒā▒ĒĢśļŖö ĒöäļĀłņ×äņØś Ļ░ĢļÅäļź╝ ņĀüņĀłĒĢśĻ▓ī ņäżĻ│äĒĢĀ ņłś ņ׳ļÅäļĪØ ĻĖ░ņ┤ł ņ×ÉļŻīļĪ£ ĒÖ£ņÜ®ļÉĀ ņłś ņ׳ņ¢┤ ņØ┤ļÅÖĒśĢ ņåīļ░®ņÜ®ņłś ņĀĆņןĒā▒Ēü¼ņØś ņĢłņĀĢņĀü ĻĄ¼ņĪ░ ņäżĻ│äņŚÉ ĻĖ░ņŚ¼ĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż.
Figure┬Ā3.
Numerical result of case 4 in Table 1: (a) nonlinear model, (b) underestimation in case of linear PeregrineŌĆÖs model compared to nonlinear one.
Table┬Ā1.
Effects of the Position and the Height of Water Supplying Nozzle: Linear and Nonlinear PeregrineŌĆÖs Model
References
1. J. Park, S. So and T. S. Jang, ŌĆ£A Numerical Study on Hydrodynamic Force Affecting the Vertical Wall of a Portable Water Storage TankŌĆØ, Fire Science and Engineering, Vol. 31, No. 3, pp. 49-53 (2017).

2. J. Park, S. So and T. S. Jang, ŌĆ£A Numerical Investigation of Hydrodynamic Force Acting on the Vertical Wall of a Portable Water Storage Tank using a Linearized PeregrineŌĆÖs ModelŌĆØ, Fire Science and Engineering, Vol. 32, No. 1, pp. 76-80 (2018).

3. S. So, J. Park, H. G. Sung and T. S. Jang, ŌĆ£Reduction of Hydrodynamic Force Acting on the Vertical Wall of a Portable Water Storage Tank by Convex Bottom DesignŌĆØ, Fire Science and Engineering, Vol. 32, No. 6, pp. 69-73 (2018).

- TOOLS
-
METRICS

-
- 1 Crossref
- 1,980 View
- 37 Download
- Related articles in Fire Sci. Eng.