Fire Dynamics Simulator를 이용한 미분무의 분사 특성이 복사열 감쇠에 미치는 영향 검토
Examination on Effects of Spray Characteristics of Water Mist on Thermal Radiation Attenuation Using Fire Dynamics Simulator
Article information
Abstract
요 약
본 연구에서는 미분무의 분사 특성이 복사열 감쇠에 미치는 영향에 대해 Fire dynamics simulator (FDS)를 이용하여 전산시뮬레이션을 수행하였다. 미분무의 액적 크기는 100-300 µm, 공급 유량은 1-3 L/min, 분사각은 60-180° 범위로 설정하였다. 액적의 크기가 감소하고 공급 유량이 증가함에 따라 복사열 감쇠율은 증가하였다. 한편, 노즐 중심을 지난 부근에서는 분사각이 감소함에 따라, 그 이후의 위치에서는 분사각이 증가함에 따라 복사열 감쇠율이 증가하였다. 최대 복사열 감쇠율의 경우 액적 크기와 분사각이 감소하고 공급 유량이 증가함에 따라 증가하였고, 평균 복사열 감쇠율의 경우 액적 크기가 감소하고 공급 유량과 분사각이 증가함에 따라 증가하였다. 본 전산시뮬레이션 조건에서, 최대 복사열 감쇠율은 액적 크기의 비와 공급 유량의 비에 의해, 평균 복사열 감쇠율은 공급 유량의 비에 의해 크게 변화하였다. 반면, 분사각의 비에 따른 최대 및 평균 복사열 감쇠율의 변화가 가장 작은 것으로 나타났다.
Trans Abstract
ABSTRACT
In this study, numerical simulations to investigate the effects of the spray characteristics of water mist on thermal radiation attenuation were performed using fire dynamics simulator (FDS). The droplet size, flow rate, and spray angle of the water mist were 100-300 µm, 1-3 L/min, and 60-180°, respectively. As the droplet size decreased and flow rate increased, the thermal radiation attenuation increased. When the spray angles decreased and increased behind the near nozzle center and behind a certain remote distance from the nozzle center, respectively, the thermal radiation attenuation increased. The peak thermal radiation attenuation increased with decreases in droplet size and spray angle and an increase in flow rate, whereas the average thermal radiation attenuation increased with a decrease in droplet size and increases in flow rate and spray angle. Under the numerical simulation conditions of this study, the peak and average thermal radiation attenuations were significantly altered by the ratios of droplet size and flow rate and by that of flow rate, respectively. However, their variations with the ratio of spray angle were the smallest.
1. 서 론
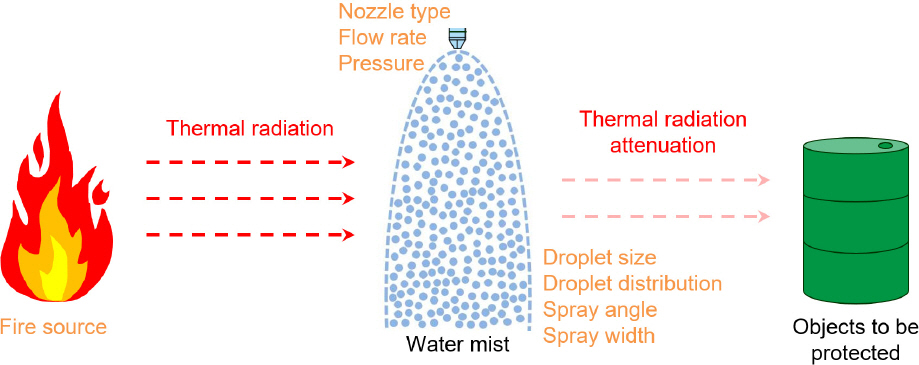
미분무(Water mist)를 이용한 미분무소화설비는 스프링클러소화설비(Sprinkler system)와 동일하게 물을 소화약제로 사용하는 설비로, 미분무는 헤드(Head)를 통해 최소설계압력 조건에서 방사된 물입자 중 99%의 누적체적분포가 400 µm 크기 이하로 방사되는 것(1)을 의미한다. 일반적으로 미분무는 화재 소화 시 화염 및 연료면의 냉각 효과, 물 액적의 기화로 인해 일어나는 부피 팽창에 의한 질식 효과, 연기나 독성 물질 차단 효과, 그리고 물 액적에 의한 복사열 흡수(Absorption) 및 산란(Scattering)으로 인한 복사열 감쇠 효과 등 다양한 효과(2-5)들을 나타낸다. 이 중 미분무에 의한 복사열 감쇠 효과는 헤드 또는 노즐(Nozzle)에서 방사된 다량의 미분무가 수막(Water curtain)을 형성하여 화원 또는 고온의 열원으로부터의 복사열을 효과적으로 감쇠시켜 위험물 시설이나 문화재 등 화재에 민감한 시설의 화재 방호 안전성을 증대시키는데 적용 가능(4,6,7)한 것으로 알려져 있다. 미분무를 이용한 복사열 감쇠에 대한 개략도를 Figure 1에 나타내었고, 미분무에 의한 복사열 감쇠 현상에 영향을 미치는 인자(Factor)로는 화원 특성, 노즐 종류, 공급 유량, 공급 압력, 액적 크기, 액적 분포, 분사각, 분무 폭 등이 있다.
기존에 미분무 또는 물분무에 의한 복사열 감쇠 성능에 대한 연구(4,8-12)가 일부 수행된 바 있다. Dembele 등(4)은 적은 체적 유량에서 작동하고 작은 액적 크기를 방사할 수 있는 2가지 종류의 단일 스프레이 노즐(Single spray nozzle)을 이용하여 액적 크기, 노즐 종류, 공급 압력 및 유량이 복사열 감쇠에 미치는 영향을 실험을 통해 확인하였다. 그 결과, 동일한 유량 조건에서 더 미세한 액적 크기를 방사하는 단일 스프레이 노즐에서 복사열 감쇠 효과가 증대되었다고 보고하였다. Murrell 등(8)은 중실원추형(Full cone type) 3종류, 중공원추형(Hollow cone type) 1종류, 총 4종류의 노즐을 이용하여 복사열 감쇠 성능을 비교하는 실험을 수행하였다. 실험 결과, 노즐을 통한 공급 압력이 증가함에 따라 공급 유량이 증가하고 액적 크기가 감소하며, 복사열 감쇠율은 증가한다고 보고하였다. Cheung(9)은 드렌처 헤드(Drencher head)를 이용하여 물분무에 의해 분사된 수막에 의한 복사열 감쇠 효과를 분석하였다. 실험 결과, 공급 압력, 공급 유량, 화원 크기가 증가함에 따라 복사열 감쇠 효과가 증가하고, 노즐의 직경이 작을수록 미세한 액적이 분사되고 더 우수한 복사열 감쇠 성능이 나타난다고 보고하였다. Chow 등(10)은 3가지 종류의 드렌처 헤드를 이용하여 복사열, 연기 및 독성 가스 차단 효과에 대한 실험을 수행하였다. 노즐 종류, 오리피스(Orifice) 직경, 공급 유량 및 압력에 의한 복사열 감쇠 효과를 확인하였으나 수막이 연속적이지 않고, 수막의 많은 공기층을 통해 연기 및 독성가스가 이동하여, 연기 및 독성 가스 차단에는 효과가 크지 않다고 보고하였다. Zhu 등(11)은 균일한 수막을 형성할 수 있도록 설계한 다중분사노즐(Multi-injector nozzle)을 이용하여 복사열 감쇠 실험을 수행하였고 해당 실험 결과를 전산시뮬레이션 결과와 비교하였다. 해당 연구에서 공급 압력이 증가함에 따라 액적 크기는 감소하고 공급 유량과 수막의 두께가 증가하여 복사열 감쇠 효과가 증가한다고 보고하였다. 한편, Balner and Barcova(12)는 단일유체노즐을 통해 분사되는 다양한 특성의 수막을 이용하여 복사열 감쇠에 미치는 효과를 평가하였다. 실험 결과, 오리피스 직경이 증가함에 따라 복사열 차단 효과가 증가하였는데, 이러한 경향이 나타난 이유에 대해 오리피스 직경 증가에 따라 액적 크기가 증가했지만 많은 유량과 넓은 액적 분포가 복사열 감쇠에 더 큰 영향을 미칠 수 있기 때문이라 보고하였다. 복사열 감쇠에 대한 액적 크기 영향만을 고려한다면, 액적 크기가 증가했음에도 불구하고 복사열 감쇠율이 증대된 이러한 기존 연구 결과(12)는 액적 크기가 작아짐에 따라 복사열 감쇠율이 증대된 기존 연구 결과들(4,8,9,11)과 차이가 있는 것처럼 보인다. 기존 연구 결과들 간 이러한 차이가 나타나는 이유는 복사열 감쇠에 영향을 미치는 미분무의 분사 특성들이 독립적이 아니라 상호 연관되어 있기 때문으로 판단된다. 예를 들면, 기존 연구에서 사용한 헤드나 노즐의 경우 대부분 동일한 오리피스 크기 조건에서 공급 압력이 증가함에 따라 공급 유량이 증가하고 액적 크기는 감소한다. 또한, 분사각도 변할 수 있다. 즉, 미분무 분사 조건 및 특성이 서로 밀접하게 연관되어 있어서 기존 연구를 토대로 복사열 감쇠에 대한 미분무 분사 특성의 독립적인 영향 평가는 한계가 있다고 판단된다. 더욱이 실험을 통해 미분무의 분사 특성이 미분무 복사열 감쇠 효과에 미치는 영향을 미분무 분사 특성(예를 들면, 액적 크기, 공급 유량, 분사각 등)에 따라 독립적으로 평가한다는 것은 매우 많은 노력이 필요하다. 하지만 전산시뮬레이션(Numerical simulation)을 이용할 경우 미분무의 분사 특성이 복사열 감쇠 효과에 미치는 영향을 독립적으로 검토 가능하다는 장점이 있으므로 전산시뮬레이션을 이용한 연구가 좋은 대안이 될 수 있다.
최근 Ko(13)는 Fire dynamics simulator (FDS)를 이용하여 미세 물분무가 복사열 감쇠에 미치는 영향에 대한 연구를 수행한 바 있다. 기존 실험 연구(8)를 대상으로 전산시뮬레이션을 수행하여 액적 직경, 분사 유량, 분사각 등의 조건에 대한 복사열 감쇠 경향을 분석하였고, 그 결과 액적 크기가 감소하고, 분사 유량과 분사각이 증가할수록 복사 감쇠가 증가하는 기존 연구(4,8,9,11)와 동일한 경향을 확인하였다. 즉, Ko(13)의 연구를 통해 미세 물분무를 이용한 복사열 감쇠 성능 예측에 대한 FDS의 신뢰성을 확인할 수 있었다. 하지만, Ko(13)의 연구에서 미세 물분무의 분사 특성들이 복사열 감쇠 효과에 정량적으로 얼마나 영향을 미치는지, 어떠한 특성들이 지배적으로 복사열 감쇠율에 영향을 미치는지에 대한 체계적인 연구가 수행되지는 않았다. 따라서 미분무에 의한 복사열 감쇠 성능을 극대화하기 위해서는 복사열 감쇠에 대한 각 분사 특성들의 독립적인 영향 평가가 체계적으로 수행될 필요가 있다고 판단된다.
본 연구에서는 미분무 분사 특성이 복사열 감쇠 효과에 미치는 영향에 대해 FDS를 이용하여 검토하였다. 기존 연구(8,13)를 토대로 전산시뮬레이션 조건을 구축하였고, 기존 연구(8)와의 비교를 통해 본 전산시뮬레이션의 신뢰성을 평가하였다. 이후, 액적 크기, 공급 유량, 분사각과 같은 미분무 분사 특성이 복사열 감쇠 성능(즉, 위치에 따른 복사열 감쇠율, 최대 및 평균 복사열 감쇠율)에 미치는 영향을 독립적으로 검토하였다. 액적 크기, 공급 유량, 분사각과 같은 미분무 분사 특성 조건의 경우, 기존 연구들의 조건들을 고려하여 설정하였으며, 각 특성들의 최소 조건을 기준으로 각각 2배 및 3배 증가시킨 조건들로 구성하여 동일한 비율의 각 미분무 분사 조건 변화에 따른 다양한 복사열 감쇠율의 변화를 비교 및 검토하였다.
2. 전산시뮬레이션 조건 및 결과 처리 방법
2.1 전산시뮬레이션 조건
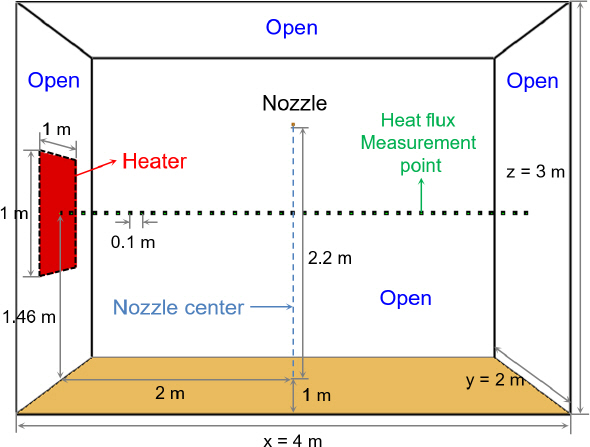
본 연구에서 구축한 전산시뮬레이션의 개략도를 Figure 2에 나타내었다. 본 연구에서는 기존 연구 결과와의 비교를 통한 본 전산시뮬레이션의 신뢰성 평가를 위해 기존 연구(8,13)를 토대로 전산시뮬레이션의 형상 및 조건을 설정하였다. 전산시뮬레이션 영역의 크기는 4 m (가로) × 2 m (세로) × 3 m (높이)이고, 바닥면을 제외한 모든 면을 개방하였다. 히터(Heater)의 크기는 1 m × 1 m, 표면 온도는 900 ℃로 기존 실험(8)과 동일하게 설정하였다. 노즐은 구획실의 중앙에 바닥으로부터 2.2 m 높이에 설치하였고, 바닥으로부터 1.46 m 높이의 히터 중심에서 0.1 m 간격으로 복사열유속을 측정할 수 있도록 설정하였다.
Table 1에 본 연구에서 설정한 전산시뮬레이션의 조건을 나타내었다. 본 연구에서는 미분무의 액적 크기, 공급 유량, 분사각이 복사열 감쇠에 미치는 영향에 대해 평가하였다. 기존 연구 검토 결과를 토대로 액적 크기는 100-300 µm, 공급 유량은 1-3 L/min, 분사각은 60-180° 범위로 설정하였다. 액적 크기 영향 파악을 위해 공급 유량 및 분사각은 2 L/min과 120°인 조건에서 100, 200, 300 µm인 경우를 설정하였고, 공급 유량 영향 파악을 위해 액적 크기 및 분사각은 200 µm와 120°인 조건에서 1, 2, 3 L/min인 경우를 설정하였으며, 분사각 영향 파악을 위해 액적 크기 및 공급 유량이 200 µm와 2 L/min인 조건에서 60, 120, 180°의 경우에 대해 전산시뮬레이션을 수행하였다. 초기 분사 속도(Injection velocity)는 2 m/s로 설정하였고, 기존 연구(8)에서 사용한 열원(즉, 히터)이 연료로 천연가스(Natural gas)를 이용하였다는 점을 고려하여 본 전산시뮬레이션에서 연료는 천연가스를 적용하였다. 본 연구에서는 전산시뮬레이션을 위해 FDS (Ver. 6.5.3)를 사용하였다.
2.2 전산시뮬레이션 결과 처리 방법
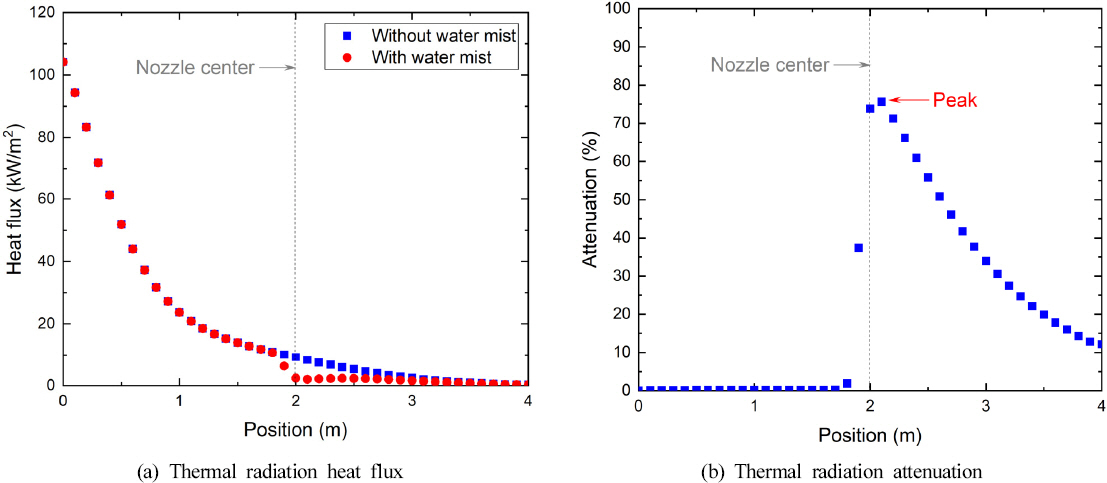
전산시뮬레이션 결과 처리 방법 설명을 위해, Figure 3에 본 연구의 전산시뮬레이션 조건 중, 액적 크기 100 µm, 공급 유량 2 L/min, 분사각 120°인 경우에 대한 전산시뮬레이션 결과를 대표적으로 나타내었다. 모든 전산시뮬레이션 결과는 복사열유속이 정상상태(Steady state)에 도달한 이후의 결과를 평균하여 나타내었다. Figure 3(a)에는 위치에 따른 복사열유속 측정 결과를 나타내었다. 미분무가 분사되지 않는 조건에서는 열원으로부터 거리가 증가함에 따라 지속적으로 복사열유속이 감소하는 경향이 관찰되었다. 미분무가 분사되는 조건에서도 노즐 중심(즉, 2 m) 부근 전까지는 열원으로부터 거리가 멀어짐에 따라 복사열유속이 지속적으로 감소하였고, 거리에 따른 복사열유속의 변화는 미분무가 분사되지 않는 조건과 유사하였다. 이러한 경향이 나타난 이유는 해당 위치에서는 미분무가 분사되지 않기 때문이다. 그러나, 미분무가 분사되는 조건의 경우 노즐 중심 부근에서 급격하게 복사열유속이 감소하는 경향이 관찰되었고, 이는 미분무의 복사열유속 감쇠 효과 때문으로 판단된다. 이러한 전체적인 경향은 본 연구의 모든 전산시뮬레이션 조건에서 유사하게 관찰되었다.
Exemplified numerical simulation result for data reduction (Droplet size = 100 µm, flow rate = 2 L/min, spray angle = 120°).
한편, Figure 3(a)를 바탕으로 본 연구에서는 Figure 3(b)에 나타낸 바와 같이 위치에 따른 복사열 감쇠율 변화 그래프를 도출하였다. 본 연구에서 복사열 감쇠율(Attenuation, γ)은 기존 연구(13)를 바탕으로 식(1)과 같이 계산하였다.
여기서, U0 와 U 는 각각 미분무가 분사되지 않는 조건과 미분무가 분사되는 조건에서의 복사열유속을 의미한다. 해당 그래프를 이용하여 미분무 분사 조건에 따른 최대 복사열 감쇠율과 평균 복사열 감쇠율을 도출하여 비교 및 검토하였다. 최대 복사열 감쇠율은 Figure 3(b)에서 나타낸 바와 같이 위치에 따른 복사열 감쇠율에서 최댓값(Peak attenuation)을 의미한다. 본 전산시뮬레이션에서 복사열 감쇠율의 최댓값은 노즐 중심을 약간 지난 부근에서 관찰되었다. 본 전산시뮬레이션에서 대상으로 한 노즐의 경우 노즐 중심에서 크기가 작은 액적이 분포(13)하고 분사 유량이 노즐 중심에 집중되는 경향을 보이므로 노즐 중심을 지난 부근(즉, 노즐 중심으로부터 오른쪽으로 약간 떨어진 지점)에서 최대 복사열 감쇠율이 나타나는 것으로 판단된다. 하지만 FDS의 신뢰성 등을 고려할 때 최대 복사열 감쇠율이 나타나는 정확한 위치에 대해서는 추후 추가적인 검토가 필요할 것으로 생각된다. 한편, 평균 복사열 감쇠율(Average attenuation, γave)은 위치에 따른 복사열 감쇠율을 전체 평균한 것을 의미하고, 식(2)를 이용하여 계산하였다.
여기서, N은 데이터 개수(즉, Figure 2에서 측정 위치 수)를 나타낸다.
2.3 전산시뮬레이션의 격자 크기 및 신뢰성 검토
전산시뮬레이션을 위한 격자 크기 설정을 위해 3가지 종류의 격자 크기 영향에 대해 검토하였다. 기존 연구(8,13)에서 사용한 중실원추형 노즐인 Nozzle D의 결과 중 압력 조건이 4 bar인 경우에 대해 정사각 형태의 격자 한 변의 길이를 0.1, 0.05, 0.033 m로 변화시켜 복사열 감쇠율에 대한 전산시뮬레이션을 수행하였고, 해당 결과를 Figure 4에 나타내었다.
비교 결과 격자 크기가 0.1 m인 경우와 0.05 m인 경우에서 최대 복사율 감쇠율이 유사한 것으로 관찰되었고 이에 비해 격자 크기가 0.033 m의 경우에서는 최대 복사율 감쇠율이 낮은 것으로 나타났다. 반면, 노즐 중심을 지난 이후 위치에 따른 복사열 감쇠율은 격자 크기가 0.05 m인 경우와 0.033 m인 경우가 절댓값의 차이는 있으나 유사한 경향을 나타내었고, 격자 크기가 0.1 m인 경우에서는 다른 두 격자 크기 경우에 비해 위치에 따른 복사열 감쇠율이 비교적 서서히 감소하는 것으로 관찰되었다.
또한, 본 전산시뮬레이션의 격자 크기 및 신뢰성을 검토하기 위해 기존 연구(13)에서와 유사하게 기존 실험 결과(8)와 본 전산시뮬레이션 결과의 비교를 수행하였다. Figure 4와 동일하게 정사각 형태의 격자 한 변의 길이를 0.1, 0.05, 0.033 m인 경우로 설정하여 전산시뮬레이션을 수행하였고, 기존 연구(8,13)에서 사용한 노즐 중 중실원추형 노즐인 Nozzle D의 결과를 대상으로 공급 유량과 공급 압력에 따른 미분무의 복사열 감쇠율의 비교 결과를 Figure 5(a)와 5(b)에 각각 나타내었다. 본 전산시뮬레이션 및 기존 실험(8) 결과 모두에서 공급 유량 및 공급 압력이 증가함에 따라 복사열 감쇠율이 증가하는 경향이 관찰되었다. 한편, 본 전산시뮬레이션과 기존 실험(8) 결과에 대한 정량적인 차이(δ)를 식(3)을 이용하여 계산하였다.

Comparison of thermal radiation attenuation between present numerical simulation and previous experimental data.
여기서 ϒnum 과 ϒexp 는 각각 본 전산시뮬레이션 및 기존 실험 연구(8)의 복사열 감쇠율 결과들을 나타낸다. 비교 결과, 본 전산시뮬레이션과 기존 실험 결과(8) 간 차이는 격자 크기가 0.1 m인 경우 약 29.0-60.0%로 평균 약 52.9%, 격자 크기가 0.05 m인 경우 약 1.4-22.0%로 평균 약 6.4%, 격자 크기가 0.033 m인 경우 약 32.9-47.0%로 평균 약 39.3%로 계산되었다.
Figure 4와 Figure 5의 검토 결과와 한 변의 길이가 0.05 m인 정사각 형태의 격자를 이용한 기존 전산시뮬레이션 연구(13), 그리고 전산시뮬레이션의 효율성 등을 고려하여 본 연구에서는 격자 크기를 0.05 m × 0.05 m × 0.05 m로 설정하였고, 이 경우 전산시뮬레이션에 사용된 총 격자수는 192,000개이다. Figure 5에 나타낸 바와 같이, 본 전산시뮬레이션과 기존 실험 결과(8) 간 전체적인 데이터의 경향 및 수치적 차이를 고려할 때 본 연구에서 구축한 전산시뮬레이션 방법이 적절하다고 판단되었고, 이후 이러한 전산시뮬레이션 방법을 이용하여 미분무의 액적 크기, 공급 유량, 분사각이 복사열 감쇠에 미치는 영향에 대해 검토하였다.
3. 전산시뮬레이션 결과
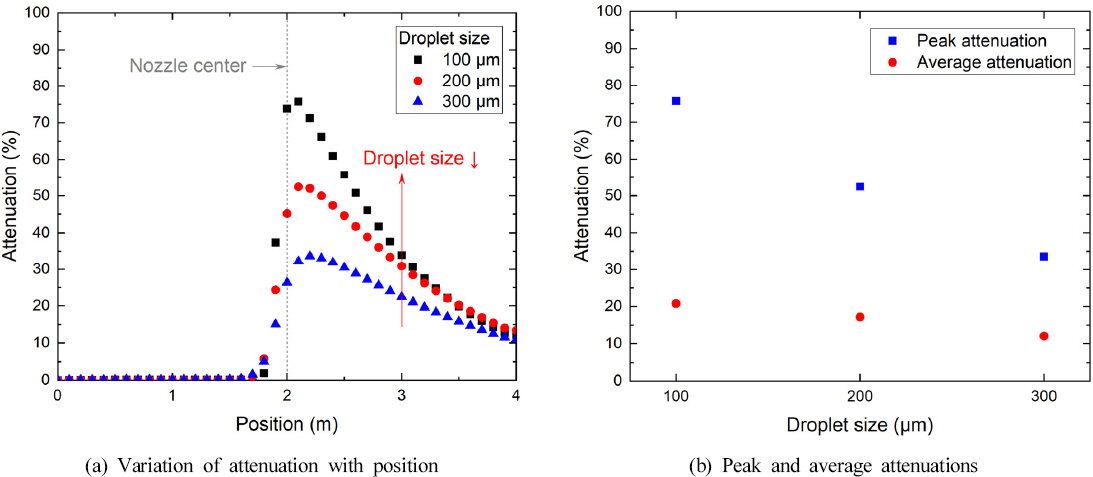
Figure 6에 복사열 감쇠율에 대한 액적 크기의 영향을 나타내었다. 공급 유량 2 L/min, 분사각 120°인 조건에서 액적 크기 100, 200, 300 µm에 따른 복사열 감쇠율을 검토하였다.
Figure 6(a)에 미분무의 액적 크기가 복사열 감쇠율에 미치는 영향을 위치에 따라 나타내었다. 노즐 중심 직전에서부터 미분무에 의한 복사열 감쇠율이 급격하게 증가하였고, 노즐 중심을 약간 지난 부근에서 최댓값에 도달하며, 이후 거리가 증가함에 따라 서서히 감소하는 경향이 관찰되었다. 액적 크기가 감소함에 따라 복사열 감쇠율은 증가하였는데, 이는 액적 크기가 감소하면 복사열을 흡수하는 액적의 개수 및 표면적이 증가하고, 액적 크기 감소에 의해 복사열 감쇠가 일어나는 특정 공간에서의 액적 체류 시간이 길어질 수 있기 때문으로 판단된다(13-15). 한편, 노즐 중심 직후 부근에서 미분무 액적 크기의 영향이 크게 나타났고(즉, 액적 크기 간 복사열 감쇠율 차이가 크게 나타났고), 노즐 중심으로부터 거리가 멀어짐에 따라 미분무 액적 크기의 영향은 감소하는 것으로 관찰되었다.
Figure 6(b)에 미분무 액적 크기에 따른 최대 및 평균 복사열 감쇠율을 나타내었다. 액적 크기가 감소함에 따라 최대 및 평균 복사열 감쇠율은 증가하는 것으로 나타났고, 액적 크기에 따른 최대 복사열 감쇠율의 변화율이 평균 복사열 감쇠율의 변화율에 비해 큰 것으로 관찰되었다. 본 전산시뮬레이션 조건에서 최대 복사열 감쇠율은 약 33.7-75.6%, 평균 복사열 감쇠율은 약 12.1-20.8%로 나타났다.
Figure 7에는 복사열 감쇠율에 대한 공급 유량의 영향을 나타내었다. 액적 크기 200 µm, 분사각 120°인 조건에서 공급 유량 1, 2, 3 L/min인 경우에 대해 복사열 감쇠율을 검토하였다.
Figure 7(a)에 공급 유량이 복사열 감쇠율에 미치는 영향을 위치에 따라 나타내었다. 액적 크기에 따른 위치별 복사열 감쇠율의 변화와 유사하게 노즐 중심 직전에서부터 미분무에 의한 복사열 감쇠율이 급격하게 증가하였고, 노즐 중심을 약간 지난 부근에서 최댓값에 도달한 이후, 거리가 증가함에 따라 서서히 감소하는 경향이 관찰되었다. 공급 유량이 증가함에 따라 복사열 감쇠율이 증가하는 경향이 관찰되었고, 이는 공급 유량이 증가에 따라 복사열을 감쇠시킬 수 있는 액적 밀도(또는 개수)가 증가하기 때문으로 판단된다.
Figure 7(b)에 공급 유량에 따른 최대 및 평균 복사열 감쇠율을 나타내었다. 공급 유량이 증가함에 따라 최대 및 평균 복사열 감쇠율은 증가하는 것으로 나타났고, 본 전산시뮬레이션 조건에서 최대 복사열 감쇠율은 약 39.2-61.7%, 평균 복사열 감쇠율은 약 11.9-20.9%로 나타났다.
Figure 8에는 복사열 감쇠율에 대한 분사각의 영향을 나타내었다. 액적 크기 200 µm, 공급 유량 2 L/min인 조건에서 분사각 60, 120, 180°인 경우에 대해 복사열 감쇠율을 검토하였다.
Figure 8(a)에 미분무의 분사각이 복사열 감쇠율에 미치는 영향을 위치에 따라 나타내었다. 노즐 중심 직전에서부터 복사열 감쇠율이 급격하게 증가하였고, 노즐 중심을 약간 지난 부근에서 최댓값에 도달, 이후 거리가 증가함에 따라 서서히 감소하는 전체적인 경향은 Figure 6(a) 및 7(a)와 동일하였다. 그러나, 위치에 따라 분사각이 복사열 감쇠율에 미치는 영향이 다르게 나타났다. 노즐 중심을 지난 부근에서는 분사각이 감소함에 따라 복사열 감쇠율이 증가하였는데 이는 분사각이 감소함에 따라 노즐 중심축 부근에서 복사열을 감쇠시킬 수 있는 액적의 밀도가 증가하기 때문으로 판단된다. 반면, 노즐 중심으로부터 일정 거리 이상에서는 분사각이 증가할수록 복사열 감쇠율이 증가하는 경향이 관찰되었는데 이는 분사각이 증가함에 따라 복사열을 감쇠시킬 수 있는 미분무 경로(즉, 분무 폭)가 증가하기 때문으로 판단된다.
Figure 8(b)에 분사각에 따른 최대 및 평균 복사열 감쇠율을 나타내었다. 액적 크기(Figure 6(b))와 공급 유량(Figure 7(b)) 변화에 따라 최대 및 평균 복사열 감쇠율이 동일한 경향을 나타낸 반면, 분사각 변화에 따른 최대 및 평균 복사열 감쇠율은 다른 경향을 나타냈다. 즉, 분사각이 증가함에 따라 최대 복사열 감쇠율은 감소하는 반면, 평균 복사열 감쇠율은 증가하는 경향이 관찰되었다. 이러한 이유는 Figure 8(a)에 대한 설명에서 언급한 바와 같이 분사각 증가에 따라 노즐 중심에서의 미분무 액적 밀도는 감소하고, 복사열이 감쇠되는 미분무 경로는 증가하기 때문으로 생각된다. 본 전산시뮬레이션 조건에서 최대 복사열 감쇠율은 약 51.3-57.7%, 평균 복사열 감쇠율은 약 15.0-17.8%로 나타났다.
한편, 본 논문에서는 미분무의 액적 크기, 공급 유량, 분사각을 최솟값에 비해 2배, 3배 변화시켜 해당 특성들에 대한 복사열 감소율의 변화를 평가하였다. Figure 9에는 미분무의 액적 크기, 공급 유량, 분사각의 비(Ratio)에 따른 복사열 감쇠율의 변화를 비교하여 나타내었다. x축에는 식(4)를 이용하여 계산한 각 특성의 최솟값을 기준으로 각 특성의 변화량을 비(Parametric ratio, α)로 나타내었다. 한편, y축에는 식(5)를 이용하여 계산한 각 특성들의 최솟값 조건에서의 복사열 감쇠율을 토대로 각 특성의 변화에 따른 복사열 감쇠율의 변화(Attenuation change, ε)를 나타내었다.
여기서 φ는 미분무의 분사 특성(즉, 액적 크기, 공급 유량, 분사각)을 의미하고 하첨자 min은 각 미분무 분사 특성의 최솟값인 액적 크기 100 µm, 공급 유량 1 L/min, 분사각 60°인 조건을 의미한다. 한편, ϒφ = min 은 각 미분무 특성이 최솟값인 조건에서의 복사열 감쇠율을 의미한다.
Figure 9(a)에 미분무의 각 분사 특성의 비에 따른 최대 복사열 감쇠율 변화에 대한 결과를 나타내었다. 공급 유량이 증가함에 따라 최대 복사열 감쇠율이 증가하였고, 최소 공급 유량(1 L/min)에 비해 공급 유량이 2배(α = 2)와 3배(α = 3)로 증가함에 따라 최대 복사열 감쇠율은 최소 공급 유량 조건에서의 최대 복사열 감쇠율에 비해 각각 약 33.9%와 약 57.4% 증가하는 것으로 나타났다. 반면, 액적 크기와 분사각이 증가함에 따라 최대 복사열 감쇠율은 감소하는 것으로 나타났다. 최소 액적 크기(100 µm) 및 최소 분사각(60°)인 조건에서의 최대 복사열 감쇠율에 비해, 각 특성들의 값이 2배 증가하였을 때 각각 약 30.7%와 약 9.1%, 3배 증가하였을 때 각각 약 55.5%와 약 11%의 최대 복사열 감쇠율 감소가 관찰되었다. 본 결과를 토대로 볼 때 액적 크기의 비와 공급 유량의 비에 의해 최대 복사열 감쇠율이 크게 변화하였고, 분사각의 비에 의한 최대 복사열 감쇠율 변화는 비교적 작은 것으로 나타났다.
Figure 9(b)에 미분무의 각 분사 특성의 비에 따른 평균 복사열 감쇠율 변화에 대한 결과를 나타내었다. 공급 유량 증가에 따라 평균 복사열 감쇠율은 증가한 반면, 액적 크기 증가에 따라 평균 복사열 감쇠율은 감소하였다. 이러한 경향은 Figure 9(a)에 나타낸 공급 유량 및 액적 크기 변화에 따른 최대 평균 복사열 감쇠율의 경향과 동일하다. 그러나, 분사각의 경우 분사각이 증가됨에 따라 최대 복사열 감쇠율은 감소(Figure 9(a))한 반면, 평균 복사열 감쇠율은 증가(Figure 9(b))하는 경향이 나타났다. 최소 공급 유량에 비해 공급 유량이 2배와 3배 증가함에 따라 평균 복사열 감쇠율은 최소 공급 유량 조건에서의 평균 복사열 감쇠율에 비해 각각 약 44.5%와 약 75.5% 증가하는 것으로 나타났다. 또한, 최소 분사각인 조건에서의 평균 복사열 감쇠율에 비해, 분사각이 2배, 3배 증가하였을 때 약 14.7%와 약 18.5%의 평균 복사열 감쇠율의 증가가 나타났다. 반면, 최소 액적 크기에 비해 액적 크기가 2배, 3배 증가함에 따라 평균 복사열 감쇠율은 약 17.4%와 약 42.1% 감소하는 것으로 계산되었다. 따라서 공급 유량의 비에 의해 평균 복사열 감쇠율 변화가 가장 큰 것으로 나타났고, 분사각의 비에 의한 최대 복사열 감쇠율 변화가 가장 작은 것으로 나타났다.
4. 결 론
본 연구에서는 미분무의 분사 특성이 복사열 감쇠율에 미치는 영향에 대해 FDS를 이용하여 전산시뮬레이션을 수행하였다. 미분무의 액적 크기는 100-300 µm, 공급 유량은 1-3 L/min, 분사각은 60-180° 범위로 설정하였고, 미분무의 분사 특성이 위치에 따른 복사열 감쇠율, 최대 및 평균 복사열 감쇠율에 미치는 영향을 검토하였다. 본 연구를 통해 도출된 주요 결과를 다음과 같이 정리하였다.
1) 액적의 크기가 감소함에 따라 복사열 감쇠율은 증가하였고, 이는 복사열을 흡수하는 액적의 개수 및 표면적이 증가하고 액적 체류 시간이 길어질 수 있기 때문으로 판단된다. 액적 크기 변화에 따른 최대 및 평균 복사열 감쇠율은 약 33.7-75.6%와 약 12.1-20.8%로 나타났다.
2) 공급 유량이 증가함에 따라 복사열 감쇠율은 증가하였고, 이는 복사열을 차단할 수 있는 액적 밀도가 증가하기 때문으로 판단된다. 공급 유량 변화에 따른 최대 및 평균 복사열 감쇠율은 각각 약 39.2-61.7%와 약 11.9-20.9%로 나타났다.
3) 분사각 영향의 경우, 분사각이 감소함에 따라 노즐 중심을 지난 부근에서의 복사열 감쇠율이 증가하였는데 이는 노즐 중심축 부근에 복사열을 감쇠시킬 수 있는 액적의 밀도가 증가하기 때문으로 판단된다. 반면, 분사각이 증가할수록 노즐 중심으로부터 일정 거리 이상에서의 복사열 감쇠율이 증가하였는데 이는 복사열이 감쇠되는 미분무 경로가 증가하기 때문으로 판단된다. 분사각 변화에 따른 최대 및 평균 복사열 감쇠율은 각각 약 51.3-57.7%와 약 15.0-17.8%로 나타났다.
4) 최대 복사열 감쇠율의 경우, 액적 크기의 비와 공급 유량의 비에 의해 크게 변화하였다. 최소 액적 크기 및 공급 유량 조건에서의 최대 복사열 감쇠율에 비해, 액적 크기 및 공급 유량이 3배 증가하였을 때 최대 복사열 감쇠율은 약 55.5%와 약 57.4% 증가되었다. 평균 복사열 감쇠율의 경우, 공급 유량의 비에 의해 가장 크게 변화하였는데 최소 공급 유량 조건에서의 평균 복사열 감쇠율에 비해, 공급 유량이 3배 증가하였을 때 최대 복사열 감쇠율이 약 75.5% 증가하였다. 반면, 분사각의 비에 따른 최대 및 평균 복사열 감쇠율의 변화가 가장 작은 것으로 나타났다.
본 연구에서는 기존의 실험적 연구 등에서는 명확하게 파악하기 어려웠던 액적 크기, 공급 유량, 분사각과 같은 미분무 분사 특성이 복사열 감쇠 성능(즉, 위치에 따른 복사열 감쇠율, 최대 및 평균 복사열 감쇠율)에 미치는 영향을 독립적으로 정량화하여 검토하였다. 본 연구 결과는 위험물 시설이나 문화재 등 화재에 민감한 중요 시설의 화재 방호 안전성을 확보하기 위해 미분무를 이용한 복사열 감쇠 성능을 극대화할 수 있는 노즐 개발에 대한 기초 자료로 활용될 수 있고, 미분무 관련 설비가 더욱 다양한 분야에 적용되는데 기여할 수 있을 것으로 판단된다.
Acknowledgements
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2019R1F1A1062867).