1. 서 론
우리나라의 최근 10년 연도별 구조출동 통계에 의하면, 수난 사고는 2010년 6,690건에서 2019년도 8,825건으로 증가하는 추세이다(
1). 본 연구의 배경이 되는 대표적 사고로는, 2011년 6월 급류에 빠진 구조대상자를 수중구조 활동 중 구조대원이 수로관에 휩쓸린 사고, 2020년 7월 폭우로 계곡물이 불어나 급류지역 내 물놀이 중 익수자 구조 중 수로관에 구조대원이 휩쓸린 순직 사고가 발생하였다. 이러한 수난 사고는 특히 여름철에 흔히 발생하는 국지성 호우로 예측하기 어려운 자연재해로 계곡이나 강 등 급류지역에서 종종 발생된다. 본 연구에서는 급류지역의 수로관 주변의 위험성을 computational fluid dynamics (CFD) 해석프로그램인 ANSYS R1를 활용하였다. 실제 수난사고가 일어난 현장 조사를 하고, 측정 값을 토대로 급류지역 내 수로관이 있는 교량을 월류하는 것을 가정하여 유속별 수로관 내부의 유속 분포 분석을 통해 수난 구조 시 어느 부분에서 유속이 변화하고, 위험한지 CFD 분석을 통해 알아보았다(
2).
2. 본 론
2.1 CFD 모델 설계
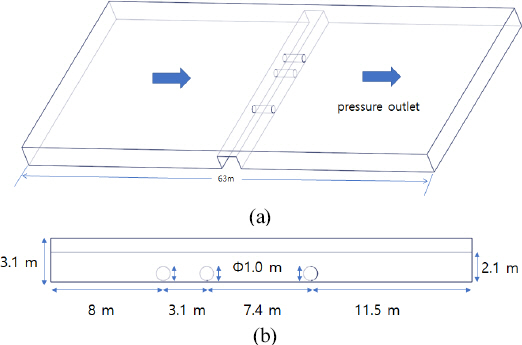
Figure 1은 전산유체역학(CFD) 수치화의 정확성을 위하여 수난 사고가 일어난 전남 구례 피아골 계곡을 찾아가 현장조사를 하여 교량의 높이와 유속을 측정하여
Figure 2와 같이 도식적으로 나타낸다. 높이는 3.1 m (교량 높이 2.1 m, 월류 높이 1.0 m), 세로 길이는 30.0 m, 가로길이는 4.0 m로 수로관의 길이와 같다. 수로관의 지름은 1.0 m이다. 현장조사 시 교량(수로관) 주변의 유속을 측정한 결과는
Figure 1에 도시하였다.
Figure 1
(a) Photos of incident site (b) Water flow velocity measurement near the bridge.

Figure 2
Modeling size of the waterway pipe inside the bridge; (a) 3-dimensional, (b) side view.
계곡은 공기와 압력의 영향을 받는 자유표면을 가지지만, 이 시뮬레이션을 할 때는 최대한 단순화하여 수로관의 유속을 측정하는 것이 목적이기 때문에 기체와 액체 사이의 계면은 고려하지 않고 모델링을 하였다.
여기서
V 2/2은 운동에너지(
V1은 교량 통과 전 물의 속력,
V2는 교량 통과 후 물의 속력), 그리고 gz는 위치에너지(g는 중력가속도, z
1은 교량통과 전의 물의 높이, z
2는 교량 통과 후의 물의 높이),
P/ρ는 유동에너지(
P1은 교량 통과 전 에너지이고,
P2는 교량 통과 후 에너지, ρ는 유체의 밀도)이며 모두 단위 질량당의 에너지이다. 따라서 베르누이 방정식은 유체가 흐름선을 그리며 흐를 때, 두 점 A와 B의 높이 그리고 두 점에서의 압력과 흐르는 속도 사이의 관계를 두 점에서 역학적 에너지가 보존됨을 바탕으로 수식으로 나타낸 것을 가리킨다(
3).
2.2 CFD 모델 설계
CFD 모델 설계는 교량 및 수로관을 측정한 것을 수치화하였다. 총 메시는 278,506개로 형성되어있으며,
Figure 3은 교량 높이 2.1 m, 간격은 8.0 m, 3.1 m, 7.4 m, 11.5 m이고, 수로관 직경은 실제 크기인 ϕ 1.0 m, 두께는 3 mm로 설정한 해석모델의 전처리 작업의 결과를 나타낸 것이다. 수로관 입구 유속은 현장조사 시 측정한 유속 값의 평균으로 산정하였다(
4).
Figure 3
Meshes of the CFD analysis model.

2.3 속도 분포
전반적인 유속 분포도를 관찰한 결과, 계곡 상류의 유속이 1.0 m/s 값이라고 가정한다면,
Figure 4에서 볼 수 있듯이 수로관을 흐르는 최대 유속은 3.0 m/s 이상인 값을 보이고, 교량의 월류높이(0.2 m)에 가까워질수록 속도가 빨라질 가능성이 있다(
4).
Figure 4
(a) Velocity distribution at the center of the water pipe (b) overflow velocity distribution.
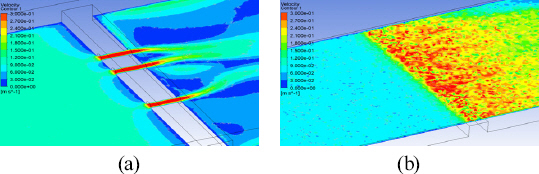
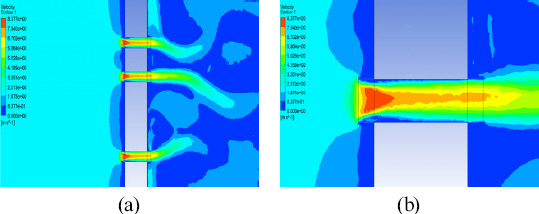
Figure 5를 보면 하천 급류시 유속이 2.0 m/s라고 가정했을 때 수로관 입구로부터 약 0.4 m 지점부터 속도가 빨라지는 것이 보였고, 내부 유속은 8.0 m/s 이상인 값을 보였다. 상류의 속도를 달리하여도 전체적인 분포는 유지가 되며 절대값만 달라지는 것을 알 수 있었다.
Figure 5
(a) Velocity distribution around the water pipe (b) magnification view of the water pipe.
2.4 수로관 입구 모형추가 속도 분포 양상
지금까지 하천 주변 및 수로관 내부 속도분포는 수로관 주변에 물체가 존재하지 않을 경우를 살펴보았다. 수로관 근처에 모형이 있다고 가정을 하는 경우 수로관 주변의 유동이 어떻게 변화할지 알아보기 위해
Figure 6에서 보이는 것처럼 CFD 모델 설계를 위하여 모형은 사람 형상을 정교하게 하기 위하여 메시의 노드 수는 95,155개, 집단은 495,542개로 형성하였다. 오차를 줄이기 위하여 continuity, x,y,z velocity에 따라 iterations를 여러 번 하였다. 여기에서도 교량 및 수로관 크기와 두께는 전과 동일한 조건으로 하고, 중력가속도 9.8 m/s
2로 설정하여 진행하였다.
Figure 6
Model meshes for the CFD analysis.

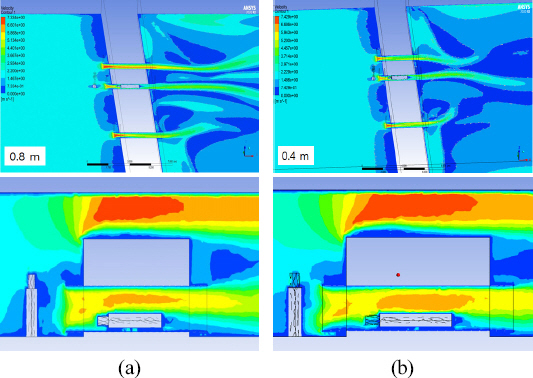
수로관 입구 주변에 모형이 있는 경우 이 모형이 수로관 입구에서 0.8 m 떨어진 경우와 0.4 m 떨어진 경우를 비교해본 결과 수로관 입구에 가까워질수록 수로관 내 유속이 빨라지고, 난류에너지 밀도가 상승하는 것을 관찰할 수 있으며, 이는 난류에너지 밀도가 클수록 난류에 의한 흔들림이 커지기 때문이라고 볼 수 있다. 수로관 내부에 모형이 있는 경우와 없는 경우를 비교해본다면 모형이 없을 때 비해 최대 유속이 8.59 m/s로 유속이 더 빨라지는 것을
Figure 7에서 확인할 수 있었다.
Figure 7
Flow velocity distribution in case of a person placed (a) at 0.8 m, (b) 0.4 m from the entrance to the water pipe.
2.5 속도장 및 압력장
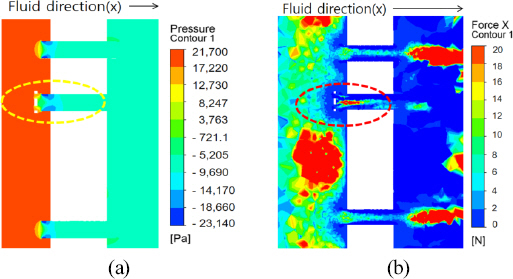
수로관 입구 쪽에 모형을 추가했을 때 속도분포를 관찰하면 수로관 근처에 가까워질수록 유속이 빨라지는 양상을 보였다. 한편, 이 모형이 받는 압력은 어떻게 변화가 될지 알아보았다. 우선,
Figure 8에서 보이는 속도장이 수로관 주변의 유체방향이 왼쪽에서 오른쪽으로 유체가 흘러간다고 가정했을 때 이 x 방향으로 압력은 9,597 N 정도이고, 이때 점성(viscous)은 유체의 흐름의 저항의 정도로 6 N을 계산을 해보면 모형에게 미치는 힘은 9,603 N 정도로 중력가속도 9.8 m/s
2를 대입해보면 960.292 N 정도의 힘을 받는 것을 알 수 있다. 모형 주변에서는 유속의 속도가 낮아지는 것을 보이고 모형을 지나자마자 유속이 8.372 m/s까지 빨라지는 것을 볼 수 있는데, 이것은
Figure 9의 압력장에서 볼 수 있듯이 압력구배(gradient)를 모형 쪽으로 이동하여 힘을 가하는 것을 측정한 것이고, 모형이 받는 압력이 더 큰 것을 알 수 있었다. 유속은 모형이 받는 힘이 커서 그 주변부만 유속이 느려지고 모형을 지나자마자 유속이 빨라지는 것을 알 수 있다(
5).
Figure 8
Velocity distribution of (a) a vertical, and (b) a horizontal section around the water pipes.

Figure 9
Fluid direction (x) around the water pipes; (a) pressure (b) force x.
2.6 난류운동에너지(turbulence kinetic energy)
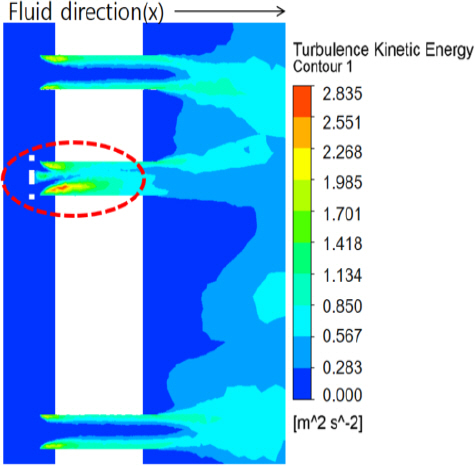
수로관 입구 쪽에 모형이 있는 경우 모형이 받는 힘이 커서 그 주변부만 유속이 느려지는 것을 확인할 수 있었으며, 이는 난류운동에너지(turbulence kinetic energy)와도 관계가 있어 측정해보았다. 난류운동에너지는 수로관 주변 모형의 각 위치에서의 평균속도에서 벗어나는 정도의 평균값이라고 보면 되는데, 이 값이 크면 난류에 의한 유동의 흔들림(drag)이 크다고 볼 수 있다.
Figures 10,
11을 보면, 모형이 수로관 입구에서 0.8 m 떨어진 난류운동에너지보다 0.4 m 떨어진 난류운동에너지의 값이 1.306에서 1.467으로 나타난다. 이것은 모형이 수로관에 가까워질수록 모형 주변 난류운동에너지 밀도가 상승하고 있다는 것을 보여준다(
6,
7).
Figure 10
Turbulence kinetic energy in the fluid (x) direction of the model around the canal pipe; (a) 0.8 m (b) 0.4 m.

Figure 11
Turbulence kinetic energy of fluid direction (x) around the water pipe.
3. 결 론
본 연구는 급류지역의 수로관 주변 위험성을 분석하였다. 전산유체역학(CFD)를 통해 분석하였으며, 급류지역의 주변 유속이 1 m/s인 경우 수로관 내부 유속은 4 m/s이고 주변 유속이 2 m/s (급류 시 유속과 유사)인 경우 수로관 내부 유속이 8.9 m/s로 주변 유속보다 수로관 내부 유속이 약 4배 정도 빠른 것을 확인하였다. 또한, 수로관 주변부에 모형이 있는 경우 모형 주변의 유속은 줄어드는 값을 보이지만 속도장 및 압력장의 영향은 크고 수로관에 가까워질수록 난류운동에너지도 밀도가 상승하는 것을 확인하였다.
따라서 급류지역 내 구조활동은 장비, 유속, 구조대상자의 위치 등을 종합적으로 고려하여 제한적으로 활동하되, 빠른 유속을 대비하여 저항을 줄이기 위해 모든 장비가 검토되어야 하며, 특히 확보 장비는 비상상황에서 잠수대원 스스로 신속하게 해제가 가능하도록 준비하고 일정 강도(구조로프 180~250 N) 이상의 장비를 사용하여야 한다. 또한, 흡입구 주변의 유속을 저하시킬 수 있는 방법을 활용하거나 유속히 완전히 느려진 후에 수행하는 것을 권고하며, 수로관의 유속이 급격하게 빨라지는 지점을 파악하고 현장지휘 및 구조활동을 하는 것이 요구된다.
본 연구는 CFD로 분석하여 수로관이 있는 급류지역의 위험성에 대하여 제시하였으며, 이를 통해 수난구조활동 시 효율성을 높일 수 있을 것으로 생각된다. 향후 급류지역 주변 지형물의 형태, 바닥면, 환경 및 구조대원 활동 조건 등을 반영하여 명확하게 파악하기 위한 추가 연구가 필요할 것으로 사료된다.
후 기
본 연구는 소방청 소방대응력 향상을 위한 연구개발지원 사업(1761002000)의 연구비 지원을 받아 수행되었습니다.
References
1. National Fire Agency. “National Fire Agency Statistical Year Book”, Vol. 137, (2020).
2. ANSYS Co. “ANSYS Ver.11”, (2007).
3. Y. A Cengel, ““Fundamentals of Fluid Mechanics, SI UNITS(Core Version)””, Mcgraw Hill Book co., USA (2018).
4. Y. S Kim, M. W Kim and Y. H Park, ““Improvement on Pressure Drop Performance of Flow Control Disk in Portable Resuscitator””, Fire Science and Engineering, Vol. 30, No. 1, pp. 1-5 (2016),
https://doi.org/10.7731/KIFSE.2016.30.1.001.

6. M. D. C Mauro, D Ken, B Mathieu, K Zahra and C Daniel, ““Comparison of CFD and One-dimensional Bernoulli Solutions of the Flow in a Plate and Frame Ultrafiltration Module in Z Configuration””, Journal of Membrane Science, Vol. 268, No. 1, pp. 74-85 (2006).

7. S. C Kim, ““Numerical Analysis of Liquid Sheet Flow around a Simplified Sprinkler Head Using a CFD Model””, Fire Science and Engineering, Vol. 30, No. 6, pp. 111-117 (2016),
https://doi.org/10.7731/KIFSE.2016.30.6.111.





