1. Y. J Kwon, “The Limit Performance of Concrete as a Fire Proof Materials and Fire Performance of Super Tall Residential Building”, Magazine of the Korea Concrete Institute, Vol. 17, No. 5, pp. 8-13 (2005),
https://doi.org/10.22636/MKCI.2005.17.5.8.

2. Y. J Kwon, J. B Jang, C. S Na and M. H Kim, “Research Trends for the Explosive Spalling of High Performance Concrete”, Magazine of the Korea Concrete Institute, Vol. 17, No. 3, pp. 20-25 (2005),
https://doi.org/10.22636/MKCI.2005.17.3.20.

3. J Lee, D Kim, S Kim, Y Kwon and K Harada, “A Study on the Effect of Compressive Strength and Water Contents on the Explosive Spalling of Concrete”, Japan Association for Fire Science and Engineering, JAFSE Annual Symposium 2009, pp. 332-333 (2009).
4. D. J Kim, B. C Han, J. Y Lee, K Harada and Y. J Kwon, “The Influence of Compressive Strength and Moisture Contents on Explosive Spalling of Concrete”, Fire Science and Engineering, Vol. 25, No. 1, pp. 42-49 (2011).
5. J. Y Lee, J. H Kim, B. C Han, S. G Park and Y. J Kwon, “A Study on the Anti-Spalling Performance of High-Strength Concrete Members by Covered Engineered Cementitious Composite”, Fire Science and Engineering, Vol. 22, No. 4, pp. 85-94 (2008).
8. D. J Kim, S. G Kang, Y. J Kwon, J. Y Lee and K Harada, “An Experimental Study on the Thermal Properties of High Strength Concrete Exposed to High Temperature”, Journal of the Korean Society of Hazard Mitigation, Vol. 12, No. 6, pp. 87-92 (2012),
https://doi.org/10.9798/KOSHAM.2012.12.6.087.

9. J. Y Lee, “An Experimental Study on the Water Vapor Pressure and Thermal Stress in the Explosive Spalling Phenomenon of High Strength Concrete During a Fire”, Doctoral thesis, Kyoto University, Japan (2016),
https://doi.org/10.14989/doctor.k19699.
10. J Blumm and A Lindemann, “Thermophysical Properties Characterization of Coarse Ceramics Using the Transient Laser Flash Technique”, J. G. Heinrich and and Aneziris, Proc 10th ECerSConf., GöllerVerlag, Baden-Baden, ISBN 3-∖4-022, Vol. 4, pp. 205-211 (2007).
11. J. C Maxwell, “A Treatise on Electricity and Magnetism”, Third Edition., Dover Publications, New York, ISBN 0-486-60636-8 (1954).
12. K HARADA and T TERAI, “A Study on Estimating the Thermal Conductivity of Concrete at High Temperature”, Architectural Institute of Japan, Kinki Chapter research meeting, Vol. 32, pp. 157-160 (1992).
13. C Tashiro, E Tazawa and Y KASAI, “Semento konkurīto-chūno mizu no kyodō, Semento konkurīto kenkyūkai mizu iinkai”, BN102⇒3, pp. 39-42 (1993), (in Japanese).
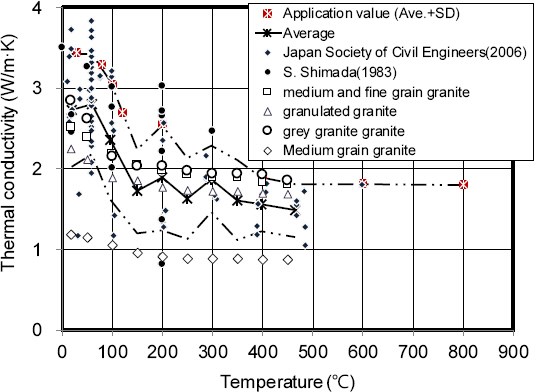
14. NFPA, SFPE Handbook of Fire Protection Engineering, (2008).
15. Journal of Japan Society of Civil Engineers (JSCE), “Netsu kankyō-ka no ganban shisetsu no kaihatsu o mezashite - netsu bussei”, ISBN 4810605272, (2006), (in Japanese).