Article information

Abstract

Trans Abstract

1. 서 론

미연연료가 가득찬 밀폐된 공간에 개구부가 개방되면 중력흐름으로 인해 공기가 유입되어지며 공간내부는 가연혼합기가 형성된다. 이후 가연혼합기에 점화가 되면 순간적으로 화재가 전파되어 공간 내부 열팽창으로 인해 구획실 내부 연료성분이 밖으로 밀려나오고 곧바로 폭발적인 화재구가 분출된다. 이러한 현상을 백드래프트(Backdraft)라고 말한다. 백드래프트는 화재진압현상에서 주로 발생하며 또한 그 피해가 크기 때문에 소방관들뿐만 아니라 건물 내 거주자들에게 큰 피해를 입힌다. 그렇기 때문에 현재까지 백드래프트에 대한 연구가 수행되어오고 있다. 하지만 백드래프트에 대한 실험연구의 경우 백드래프트의 위험성과 백드래프트 재현의 어려움으로 인해 아직까지 백드래프트에 대한 연구가 많이 진행되진 않은 상태이다.

백드래프트에 대한 연구는 Fleichmann [1]이 백드래프트 재현실험을 성공한 이후부터 본격적으로 수행되어오고 있다. Fleichmann 등[2]은 백드래프트에 대한 실험연구를 수행하였고 백드래프트의 강도를 나타내는 변수인 압력을 측정한 결과 백드래프트가 발생하는 동안 압력이 급격히 상승하는 순간이 두 번 나타난다는 것을 확인하였다. 이후 Weng과 Fan [3]도 축소 구획실을 대상으로 세로로 긴 문 형태의 개구부를 포함하여 여러 형상의 개구부에 따른 백드래프트 실험연구를 수행하였다. 그 결과 개구부 형상에 따라 백드래프트가 발생할 수 있는 구획실 내부 미연연료의 임계농도가 다르다는 것을 확인하였다.

최근에는 백드래프트에 대한 전산해석 연구도 일부 진행되고 있다. 백드래프트는 예혼합(또는 부분예혼합)화염의 특성과 확산화염의 특성을 모두 보이기 때문에 전산해석에 적용되는 연소모델의 예측성능이 매우 중요하다. 이러한 이유로 초기 백드래프트에 대한 전산해석에서는 수치적 재현성 연구와 더불어 연소모델의 성능검토와 관련된 연구가 주를 이루고 있다. 이들 연구에는 화재 전산해석에 많이 사용되는 Fire Dynamics Simulator (FDS)를 적용한 전산해석을 수행한 경우가 많은데 Park 등[4,5]은 FDS v5의 직접수치모사(Direct Numerical Simulation, DNS)와 유한화학반응(Finite chemistry reaction)을 적용하여 백드래프트 현상을 성공적으로 재현한 바 있다. 이 연구에서는 확산화염 전산해석에만 특화된 혼합분율(Mixture fraction) 연소모델은 백드래프트를 예측할 수 없음을 보인 바 있다.

Myilsamy 등[6]은 FDS v6을 이용하여 대와동모사(Large Eddy Simulation, LES) 기법과 Mixing-Controlled Fast Chemistry (MCFC) 및 Eddy Dissipation Concept (EDC) 연소모델을 적용하여 백드래프트에 대한 전산해석을 수행하였다. 이 연구에서는 유한화학반응을 고려할 수 있는 EDC 연소모델을 적용한 LES 기법으로는 백드래프트의 생성을 관찰할 수 없었고 MCFC 연소모델을 적용한 LES 기법으로만 백드래프트를 수치적으로 재현하는데 성공하였다. 그러나 기본적으로 유한화학반응을 고려하도록 모델링된 EDC 연소모델이 MCFC 연소모델보다는 진보된 모델이며, 좀 더 다양한 화재조건에 적용할 수 있는 잠재력을 가지고 있기 때문에 LES와 EDC 연소모델을 결합한 전산해석으로 백드래프트를 수행할 수 있다면 향후 연구에서 더 유익한 결과들을 얻을 수 있을 것으로 보인다.

따라서 본 연구에서는 FDS v6의 EDC 연소모델이 적용된 LES 기법을 이용하여 백드래프트 현상을 합리적으로 재현하기 위한 수치적 방법을 검토하였다. 이를 통해 EDC 연소모델을 적용한 LES 기법으로도 백드래프트를 합리적으로 예측할 수 있었으며, 기존의 실험과 MCFC 연소모델을 적용한 LES 결과와도 비교하여 그 예측성능을 검토하였다.

2. 전산해석 방법

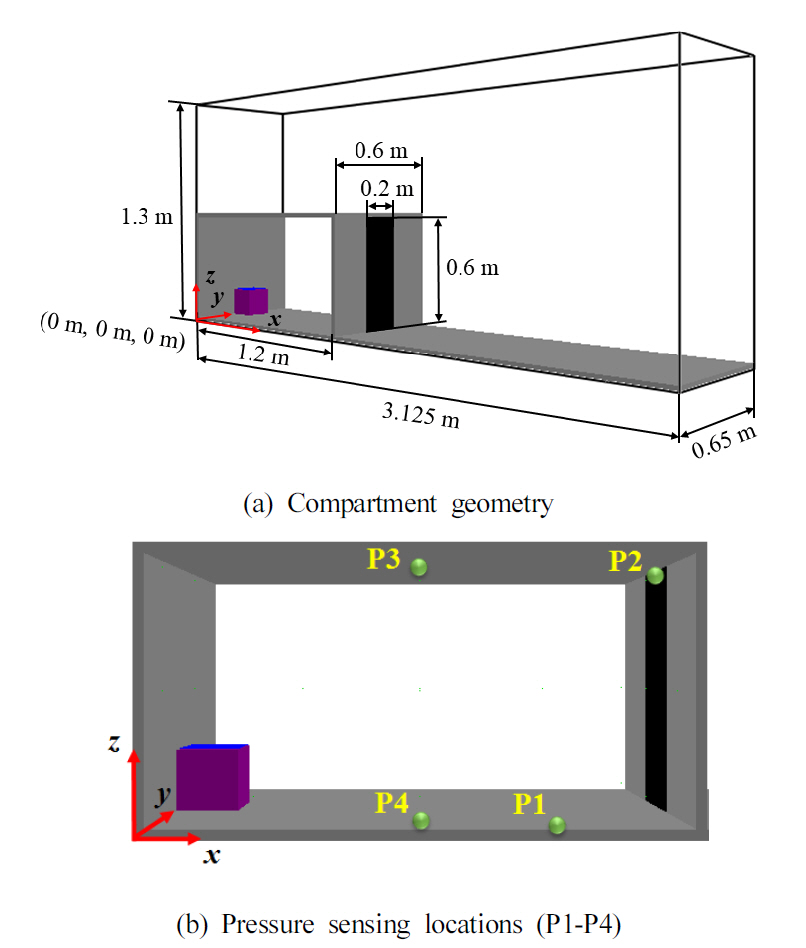
본 연구에 사용된 구획실은 Weng과 Fan [3]이 실험에서 사용한 축소규모의 구획실(1.2 m × 0.6 m × 0.6 m) 크기와 동일하며 개구부 또한 구획실 앞쪽에 세로로 긴 형상(0.2 m × 0.6 m)으로 실험과 동일하게 Figure 1 (a)와 같이 지정하였다. 구획실 가장 안쪽에는 점화를 위해 가로 × 세로 × 높이 = 0.15 m × 0.15 m × 0.15 m 크기의 점화원(정육면체)을 가운데 위치시켰다. 그리고 점화로 인한 영향을 줄이기 위해 점화원의 상부면에서 1500 ℃의 고온질소를 0.5 s간 0.05 m/s의 유속을 갖고 분사하여 점화시켰다. 점화순간은 점화원 상부면에서의 밀도가 구획실 내부로 유입된 공기로 인해 밀도가 10% 변화할 때에 지정하였다. 이를 고려하면 구획실 내부 초기조건에 따라 시간에 따른 공기유입량이 다르기 때문에[7,8] 구획실 내부 초기조건에 따라 점화순간이 달라진다. 계산영역은 백드래프트로 인한 화재구가 개구부쪽으로 분출되는 것을 고려하여 Figure 1 (a)와 같이 개구부쪽의 방향으로 구획실 가로길이의 2.5 배, 구획실 위쪽 방향으로 2 배만큼 늘려서 지정하였다. 격자크기는 기존 논문[8]에서 사용하였던 것과 동일하게 2.5 cm의 크기로 총 169,000개의 균일 격자계를 구성하였다. Figure 1 (b)에는 백드래프트 전개과정에서의 압력을 확인하기 위한 4개의 수치적 압력측정 위치(P1-P4)를 보여주고 있다. P1은 Weng과 Fan의 실험에서 압력을 측정했던 위치와 동일한 곳으로서 측벽과 바닥면이 만나는 개구부에서 멀지 않은 모서리에 위치한다. 그 정확한 좌표는 (x, y, z) = (0.925 m, 0.025 m, 0.025 m)이다. P2는 개구부 중심선의 상단부에 위치하고, P3는 천장면 중간에 위치하며, P4는 안쪽벽과 개구부면 중간에서 측벽과 바닥면이 만나는 모서리에 위치한다. 이 중에서 P2 위치는 기존의 전산해석 연구[9]에서 백드래프트의 압력을 측정하기에 적합한 것으로 알려진 위치이다.

Figure 1.

Schematic of compartment geometry and pressure sensor locations.

백드래프트에 대한 전산해석을 위한 구획실 내부의 초기조성과 온도분포는 Weng과 Fan의 실험[3]에서 얻어진 조건과 동일하도록 하였으며 구체적인 값들은 Table 1에 기술된 바와 같다. Table 1에서 보는 바와 같이 초기 구획실 내부에서 연료성분은 메탄(CH4)이다.

Table 1.

Initial Species and Temperature Conditions inside the Compartment

본 연구의 전산해석에는 NIST에서 개발된 FDS v6을 이용하였고 아격자 모델(Subgrid model)로 Deardorff’s 모델이 적용된 LES 기법을 적용하였다. 복사모델은 Gray-gas 모델을 사용하였다. 또한 백드래프트를 위한 연소모델 예측성능의 검토를 위해 기존 연구[6,8]에서 백드래프트를 합리적으로 예측하는 것으로 확인된 MCFC와 1-step 유한화학반응을 고려할 수 있는 EDC 연소모델을 새롭게 포함하여 백드래프트 수치계산을 수행하였다. 기존의 검토된 MCFC 모델은 혼합시간을 통해 단위체적당 평균반응율로 계산되는 연소모델로 혼합시간이 합리적으로 계산되었을 때 정확한 계산이 가능하지만 EDC 모델은 유한화학반응을 고려할 수 있기 때문에 적절한 반응기구를 고려하였을 때 화염에 대한 예측성능이 매우 우수하다. 통상적으로 MCFC 모델이 유한화학반응을 고려하는 EDC 모델보다 계산시간이 짧다는 장점이 있지만 다양한 혼합시간이 존재하는 화염에 대해서는 정확도가 낮아질 수 있다는 단점이 있다. 다음으로 본 연구에서 사용된 연소모델의 화학반응기구는 아래와 같다.

3. 결과 및 고찰

Figure 2는 MCFC와 EDC 1-step 연소모델을 이용하여 계산한 점화순간부터 백드래프트 발생 직후까지의 단위 체적당 열발생률(Heat Release Rate Per Unit Volume, HRRPUV)이 200 kW/m³ 이상인 영역을 나타내고 있다. HRRPUV는 반응이 가장 활발한 영역에서 높게 나타내기 때문에 HRRPUV 값이 높은 국소 영역은 화염면으로 볼 수 있어 그림의 결과를 통해 백드래프트 전개과정 동안의 화염전파거동을 잘 관찰할 수 있다. 각 계산에서 백드래프트가 발생하는 순간은 MCFC의 경우에는 6.07 s이며 EDC 1-step의 경우에는 5.84 s로서 MCFC보다 EDC 1-step 모델이 백드래프트의 발생을 약간 빨리 예측하는 것으로 나타나고 있다. 백드래프트 발생 순간을 제외하면 두 모델의 계산결과는 점화되어 상층부에 평평하게 혀모양의 화염이 전개된 후(MCFC: 3.70 s, EDC 1-step: 3.74 s) 구획실 바닥쪽으로 화염이 전파되다가 급격히 화염이 바닥근처로 확산되는 전형적인 백드래프트의 전개과정을 잘 보여주고 있다.

Figure 2.

Distribution of heat release rate per unit volume greater than 200 kW/m³ during the backdraft development for different combustion models.

백드래프트 전개 과정을 더 자세히 검토하기 위해 중간단면(y = 0.325 m)에서 시간경과에 따른 온도분포를 Figure 3에 도시하였다. Figure 3의 시간순서는 Figure 2의 HRRPUV를 도시한 시간순서와 동일하게 화염이 점화된 순간부터 나열하였다. 먼저 앞에서도 설명한 바와 같이 백드래프트가 발생하는 순간에 약간 차이가 있는 점을 제외하면 온도 분포 거시적인 전개거동은 두 모델의 계산사이에 특별한 차이는 없는 것으로 보인다. 또한 Figure 3에서 고온의 영역은 Figure 2의 HRRPUV 값이 높은 영역과 거의 일치하는 것을 알 수 있다. 다만 중간단면에서의 온도를 보면 백드래프트 발생 순간은 상부의 혀모양의 화염에서 아래로 전파되다가 바닥쪽으로 급격히 화염이 확대되는 순간(MCFC: 5.80 s-6.07 s, EDC 1-step: 5.64 s-5.84 s)에 발생하는 것을 좀 더 명확하게 보여주고 있다. 기존의 연구[8,11]에서 알려진 바에 의하면 백드래프트 발생 순간에 화염이 바닥쪽으로 급격히 전파되는 이유는 상층부에서 하층부로 전파되는 화염이 연료-공기 혼합이 잘 이루어지는 혼합층 영역에 이르게 되어 반응이 급격히 강해지게 되고 복사 열전달에 의해 바닥쪽으로 순간적인 화염확대가 이루어지기 때문이다.

Figure 3.

Temporal distributions of temperature during the backdraft development for different combustion models at a plane of y = 0.325 m.

Figure 4는 시간에 따른 압력분포 변화를 나타낸 것이다. 두 연소모델로 계산한 경우 모두 초기 점화순간에 구획실 상층부에서 압력이 증가하기 시작하여 백드래프트 발생 순간에 구획실의 바닥쪽으로 고압영역이 넓어지는 것을 알 수 있다. 이 압력분포는 Figure 3의 백드래프트 전개과정 동안의 온도분포를 통해 잘 설명될 수 있다. 점화원 근처에서 형성된 화염은 부력에 의해 구획실 상부로 이동하고 천장면을 따라 형성된 후 연료-공기 혼합기가 존재하는 아래쪽으로 전파되기 시작한다. 백드래프트 과정에서 압력이 증가하는 이유는 화염에 의한 고온 열팽창효과에 의한 것으로서 고온 화염대 영역에서 밀도가 낮아진 효과에 기인하게 된다. 초기 상층부에서 형성된 고온영역으로 인해 압력도 구획실 상층부에서부터 증가하기 시작하여 아래쪽으로 점차 고압영역이 넓어지게 되며 바닥쪽으로 고온영역이 급격히 확대되는 순간에 압력도 급격히 증가하여 화염을 개구부바깥으로 강하게 밀어내고 백드래프트가 발생하게 된다. 이러한 결과를 통해서 화염온도 분포와 압력분포 사이에는 매우 유사한 특성이 있으며 온도분포 영역을 통해서도 구획실 내부의 개략적인 압력분포 영역을 유추해 볼 수 있을 것으로 판단된다.

Figure 4.

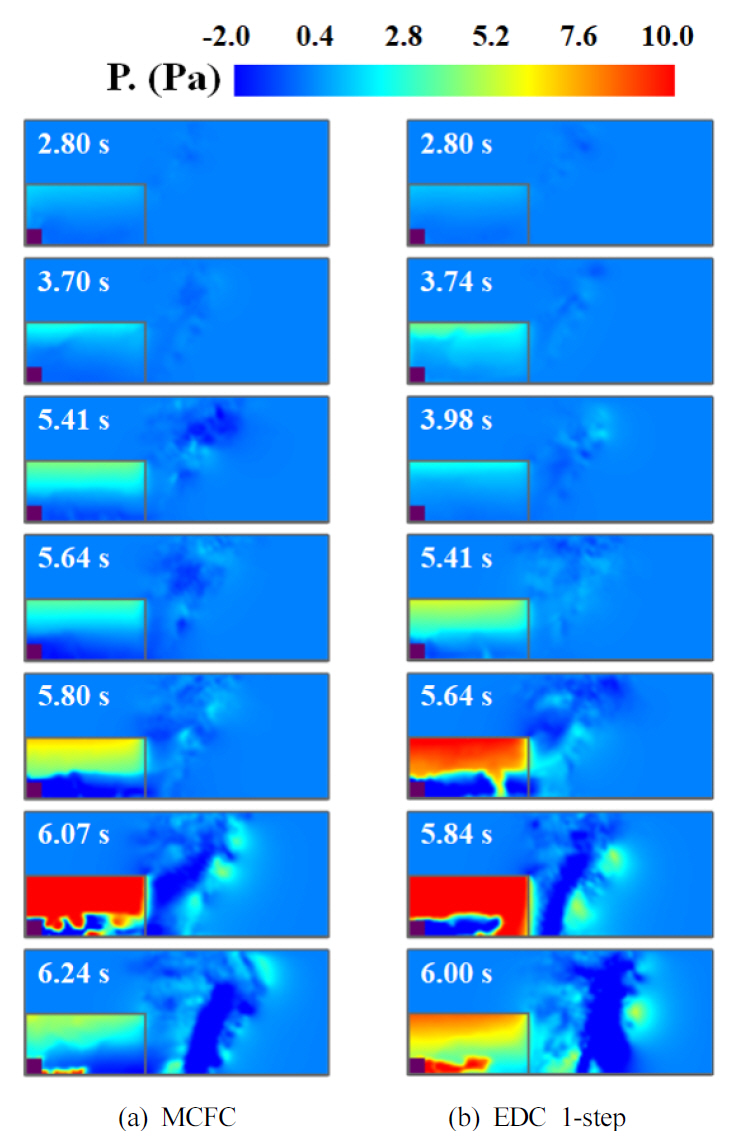
Temporal distributions of pressure during the backdraft development for different combustion models at a plane of y = 0.325 m.

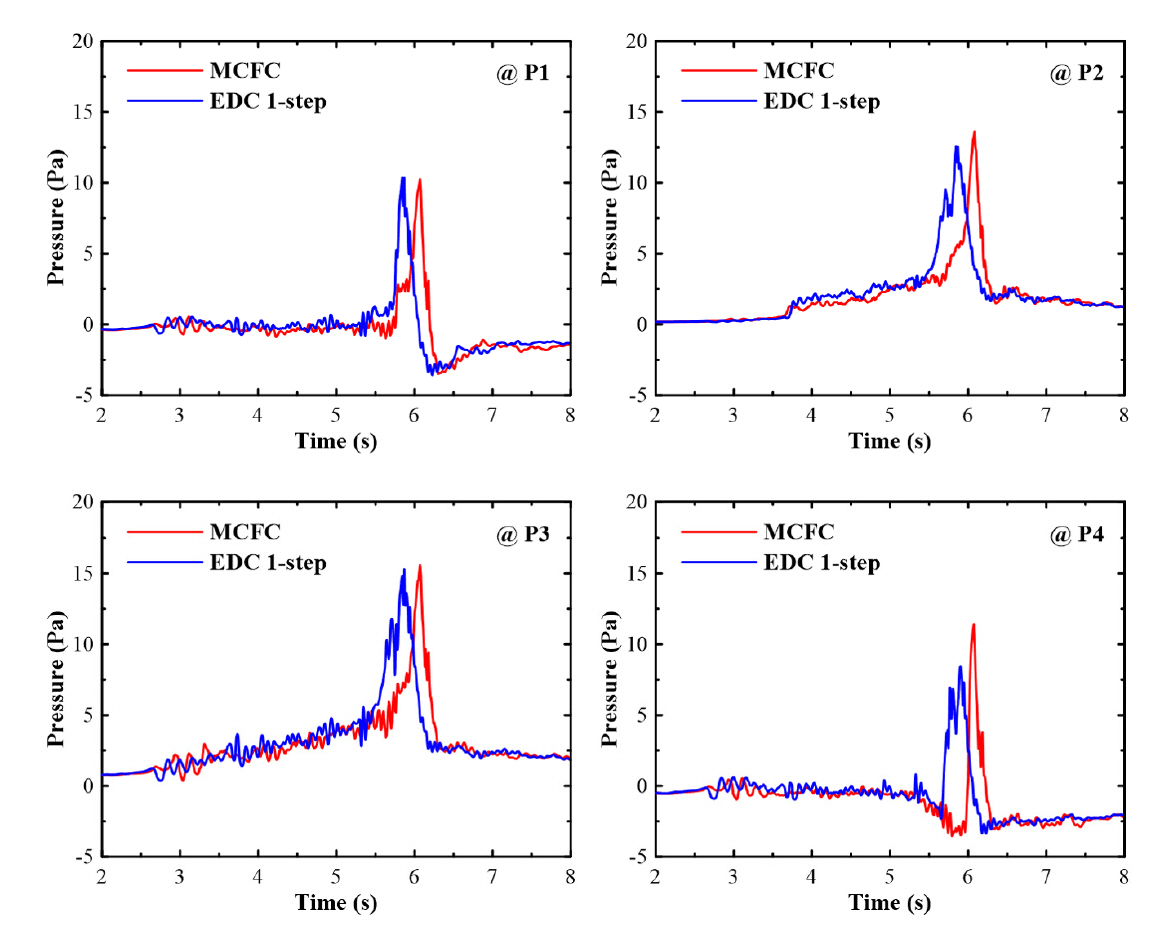
Figure 5는 P1-P4 압력센서 위치에서의 시간에 따른 압력변화를 도시한 것이다. 각 위치에 따른 압력변화를 보면 위치에 따라서 압력값 크기와 변화경향에 약간의 차이는 있음을 알 수 있다. 특히 바닥쪽에 위치하는 P1과 P4에서는 백드래프트 이후 부압을 보이고 있는데 이는 백드래프트에 의한 화재구가 분출된 이후 구획실 내부의 부압에 의해 공기가 바닥면을 타고 재 유입되는 현상을 간접적으로 보여주는 것으로서 기존의 실험결과[2]와도 잘 일치하고 있다. 두 모델간의 예측성능 차이를 고찰해보면 백드래프트가 발생하는 최고압력 순간이 약간 차이가 있음을 제외하면 큰 차이는 확인되지 않고 있다. P1 위치에 대해 실험에서 측정된 압력[3]이 7.8 Pa이고 MCFC로 계산한 경우 10.3 Pa, EDC 1-step의 경우 10.4 Pa 정도임을 고려해 본다면 EDC 1-step 모델을 포함한 전산해석도 백드래프트 발생과정의 최고압력을 정량적 측면에서도 합리적으로 예측하는 것을 알 수 있다.

Figure 5.

Temporal variation of the pressures at sensor locations of P1-P4 for different combustion models.

참고로 기존의 실험연구[2]에서는 백드래프트가 발생하는 동안 두 개의 압력피크를 확인한 바 있는데 두 연소모델을 적용한 본 연구에서는 백드래프트가 발생하기 전의 첫 번째 압력피크는 확인할 수 없었다. 백드래프트 발생순간의 압력값이 가장 중요하지만 유한화학반응기구와 DNS를 적용한 기존의 전산해석 연구[6,7]에서는 백드래프트 발생 전의 첫 번째 압력피크도 잘 모사된 바 있다. 이러한 점은 DNS와 LES의 차이 그리고 적용한 연소모델의 차이에 기인한 것으로 추정되며 향후 좀 더 구체적인 검토가 필요할 것으로 보인다. 그러나 DNS보다 계산시간이 현격히 적은 LES 계산으로도 백드래프트의 거시적인 거동과 최고압력을 합리적으로 예측할 수 있어서 FDS의 LES를 활용한 백드래프트이 전산해석은 유용할 것으로 판단된다.

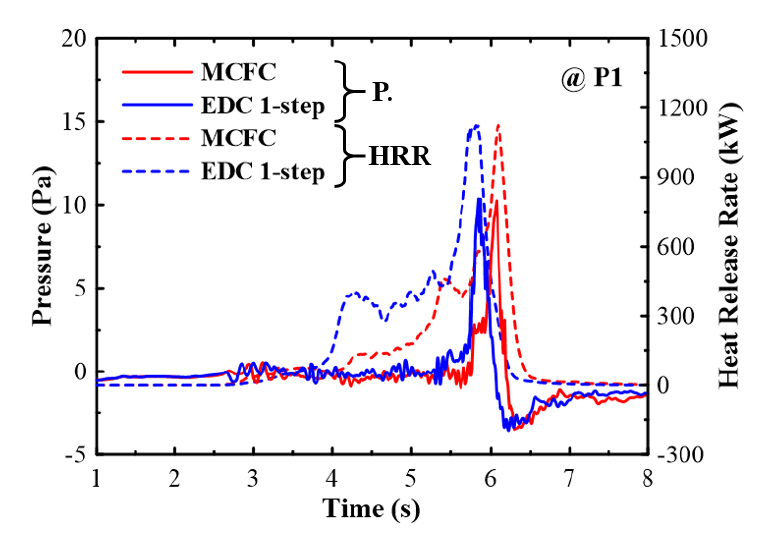
Figure 6은 P1 위치에서의 시간에 따른 압력변화와 열발생률(Heat release rate)을 도시한 것이다. 앞에서도 설명한 바와 같이 최고압력의 시점이 백드래프트가 발생하는 순간인데 이 점은 열발생률이 최고인 순간과 일치하고 있다. 열발생률이 첫 번째로 높아지는 순간에 구획실 내부에서는 연소에 의한 고온영역이 많이 형성된다는 점을 고려한다면 이 때가 첫 번째 압력피크 시점으로 유추해볼 수 있다. 열발생률 변화거동은 유한화학반응을 고려할 수 있는 EDC 1-step의 경우가 MCFC보다 좀 더 명확하게 변화하는 것으로 보여 내부의 연소상태를 파악하는데 더 유리할 것으로 추정된다. 그러나 두 모델로 예측한 압력값은 열발생률이 첫 번째로 크게 증가하는 순간에도 크게 증가하는 경향은 보이고 있지 않다. 열발생률은 구획실 내부의 연소상태를 잘 보여주는 인자이기 때문에 향후 백드래프트 전개과정에서 압력을 측정한 실험과의 비교를 통해 열발생률로도 두 개의 압력피크 점들을 유추할 수 있을지에 대해서 추가적으로 검토해 볼 필요가 있을 것으로 판단된다.

Figure 6.

Temporal variation of the pressure at P1 location and heat release rate inside the compartment for different combustion models.

4. 결 론

본 연구에서는 FDS를 이용한 기존 전산해석 연구에서 백드래프트를 예측할 수 없었던 EDC 1-step 연소모델을 이용하여 백드래프트에 대한 LES 전산해석 연구를 성공적으로 수행하였다. 기존 연구와는 달리 EDC 1-step의 유한화학반응에서 활성화에너지를 적절히 조절하여 백드래프트에 대한 예측이 가능하였다.

EDC 1-step 연소모델을 이용한 예측결과는 기존에 백드래프트에 대해 합리적인 전산해석이 가능한 것으로 알려진 MCFC 연소모델의 예측결과와 비교 검토되었다. 얻어진 결과에서는 백드래프트 발생 시점을 제외하면 EDC 1-step 결과와 MCFC 결과가 매우 유사한 것을 확인할 수 있었으며 실험의 최고 압력값을 합리적인 수준에서 예측하였다. 그러나 EDC 1-step 연소모델도 MCFC와 마찬가지로 백드래프트 전개과정의 첫 번째 압력피크에 대해서는 예측하지 못하는 것을 확인하였다. EDC 1-step의 경우 MCFC보다 시간에 따른 열발생률 변화가 좀 더 명확하게 나타나고 있고 압력변화는 구획실 내부의 연소상태와 밀접한 연관이 있기 때문에 열발생률이 백드래프트 전개과정의 압력변화와 큰 상관관계에 있는지에 대해서 추가적인 연구가 필요할 것으로 판단된다.

Article information Continued