발포 플라스틱 단열재의 표면 열분해 특성 분석 및 열분해 모델링에 관한 실험적 연구
Experimental Study on the Surface Pyrolysis Properties and Modeling of Expanded Polystyrene
Article information
Abstract
건축물의 에너지 절약을 위해 사용되는 단열재는 가연성 물질로서 화재 시 급속한 화염 전파로 인해 잠재적인 위험성을 가진다. 고체 가연물의 점화는 표면 열분해를 통해 발생하기 때문에, 고체 가연물인 단열재의 열분해 과정을 이해하는 것은 중요하다. 따라서, 본 연구에서는 단열재인 expanded polystyrene (EPS)의 열분해 현상을 분석하기 위해 thermogravimetric analysis (TGA) 실험을 수행했다. 그 결과, EPS는 약 370-430 ℃의 온도 범위에서 한 번의 질량 감소를 통해 열분해가 일어났다. TGA 실험에서 얻은 열분해 특성으로부터 model-free 법과 model-fitting 법을 사용하여 열분해 반응속도를 분석하였고, EPS의 열분해 물성치인 활성화 에너지와 선인자 계수, 열분해 반응 메커니즘을 도출하였다. 또한, 화재 시뮬레이션의 열분해 모델을 사용하여 도출된 열분해 물성치의 적정성을 검토했다.
Trans Abstract
Insulation materials are widely used in buildings for energy conservation. However, a combustible insulation material poses a potential risk of rapid flame propagation in the event of a fire. Since ignition occurs through surface pyrolysis before combustion takes place, it is important to understand the pyrolysis process of insulation materials. In this study, thermogravimetric analysis (TGA) was conducted at different heating rates to investigate the pyrolysis of expanded polystyrene (EPS). The results indicate that the pyrolysis of EPS occurs in one stage, with weight loss occurring at temperatures in the range of 370–430 ℃. The pyrolysis kinetics were analyzed using the model-free and model-free method based on TGA results. Kinetic analysis allowed for the determination of pyrolysis parameters such as activation energy, pre-exponential factor, and reaction mechanism of EPS. Furthermore, the suitability of the pyrolysis parameters obtained in this study was examined using a pyrolysis model for fire simulation.
1. 서 론
전 세계적으로 에너지 저감에 대한 관심과 노력이 증가하고 있다. 건축물에서는 전 세계 에너지 소비의 약 30-40%를 차지하고 있다(1,2). 건축물의 온도 조절을 통한 에너지 저감을 위해서 단열재의 중요성이 높아지고 있다. 이러한 단열재는 단열성능이 우수하고 취급 및 시공이 편리하면서 비용이 저렴하여 건축 자재로 쓰인다. 하지만, 많이 사용하고 있는 스티로폼, 우레탄폼 등의 유기 단열재는 가연성 물질로 화재 시 화염 전파가 빠르고, 연기 및 유독 가스를 다량으로 배출하는 문제가 있다. 1999년 화성 씨랜드 청소년 수련원 화재(3)를 시작으로, 2008년 이천 냉동창고 화재(4), 2017년 제천 스포츠 센터 화재(5), 2020년 이천 물류창고 화재(6)는 단열재로 인해 화재가 확대되었으며, 심각한 인명 및 재산 피해를 초래했다. 2022년 국토부에서는 건축법 개정을 통해 유기 단열재 사용을 제한했지만(7), 법 시행 이후 건물에만 적용되면서 개정 이전에 지어진 건축물은 여전히 화재에 노출되어 있어 개정 이후에도 단열재로 인한 화재가 계속해서 발생하고 있다.
단열재는 고체 가연물로서 고온 열원에 노출되면 표면에서 물리⋅화학적 변화를 겪는데, 이러한 과정은 열분해라고 한다. 고체 가연물은 열분해로 인해 표면에서 가연성 증기가 발생하고 공기와 만나 혼합되어 가연성 혼합기를 형성한다. 이 가연성 혼합기가 점화 온도에 도달하면 착화원에 의해 연소하게 된다. 연소반응으로 인해 생성된 열이 연료 표면을 재가열하여 가연성 증기의 발생을 촉진하게 되고 연소를 지속시키며 이러한 과정이 반복되어 화재가 성장하게 된다. 열분해 속도는 가연성 증기의 방출 속도를 결정짓고 그에 따라 연소 속도와 화재 성장을 결정하므로 열분해 과정에 대한 해석이 반드시 선행되어야 한다. 고체 물질의 열분해 과정을 해석하기 위해서는 열분해 특성이 요구된다. 열분해 특성은 활성화 에너지(activation energy), 선인자 계수(pre-exponential factor)와 같은 열분해 물성치로 나타나며, 이는 열중량 분석(thermogravimetric analysis, TGA) 실험을 통해 결정될 수 있다.
TGA 실험을 통한 단열재의 열분해 특성에 관한 연구는 많이 수행되고 있다. Pau 등(8)은 난연성 폴리우레탄폼과 불연성 폴리우레탄폼의 열분해 거동을 분석하고자 하였다. 세가지 그래프 기법을 적용하여 열분해 물성치를 추정하였으며, 열분해 모델에 적합한 기법을 제시하였다. Li 등(9)은 extruded polystyrene (XPS)의 반응 메커니즘을 확립하고자 하였으며, 더 정확한 열분해 물성치를 추정하기 위해 다양한 반응속도 분석법을 사용하였다. 이러한 분석법을 통해 열분해 과정을 모사할 수 있는 반응함수를 도출하였다. Hossain 등(10)은 단열재인 그라스울과 XPS의 반응속도 데이터를 조사하였다. XPS는 한 번의 반응을 가져 model-free 분석법을, 그라스울은 세 번의 반응을 겪어 model- based 분석법을 통해 열분해 물성치를 결정하였으며 분석 시 XPS는 Friedman model, 그라스울은 An model이 적합함을 제시하였다. Zhang 등(11)은 공기 조건에서 expanded polystyrene (EPS)의 열분해 반응속도와 메커니즘을 얻고자 하였고, 그 결과 EPS의 열분해 과정을 모델링 할 수 있는 반응함수를 보여주었다. Ni 등(12)은 새로운 포괄적인 방법을 사용하여 질소 및 공기 조건에서 EPS의 열분해 반응속도를 추정하였으며, 두 가지의 열분해 반응함수를 제시하였다. 선행 연구들(8,9,11,12)은 열분해 분석 결과인 열분해 물성치가 화재 시뮬레이션의 입력 인자로 사용되어 대규모 화재 시뮬레이션을 위한 가이드라인을 제공하기를 기대하였으나, 열분해 특성값만 제시할 뿐 도출된 값에 대한 검증은 이루어지지 않고 있다.
화재 시뮬레이션에서는 열분해 모델을 적용하여 고체 가연물의 열분해로 인한 주변 환경의 영향을 고려할 수 있다. 화재의 주변 환경에 대한 영향을 고려하면 화염 전파 및 표면에서의 가연성 증기 생성과 같은 현상을 해석할 수 있다. Prasad 등(13)은 폴리우레탄폼 슬래브에 대한 화재 확산을 모델링 하기 위해 Gpyro 소프트웨어로부터 TGA 결과에 대해 산출된 열분해 물성치를 fire dynamics simulator (FDS)의 입력 인자로 적용하였다. 1차원 모델뿐만 아니라 2차원 및 3차원 모델에 대해 시뮬레이션을 수행하여 실험에서 관찰된 화염 전파 결과를 비교하였다. 이 연구를 통해 화재 시뮬레이션이 실험보다 화염 전파 속도가 최소 2배 빠르게 예측하는 것으로 나타났다. 이처럼, 고체 가연물 중 단열재를 대상으로 열분해 모델을 적용하여 화재를 해석한 연구는 부족한 실정이다. 또한, 열분해 모델의 입력인자로 사용되는 열분해 물성치를 산출하는 데 어려움이 있어 열분해 현상을 고려하지 않거나 복잡한 열분해 반응을 단순화하여 해석하고 있다. 하지만, 화재 시 급속한 화염 전파를 일으키는 단열재는 열분해 모델을 적용하여 상세한 화재 현상을 구현해야 한다. 또한, 추후 FDS의 열분해 모델을 통해 단열재의 연소 특성을 구현하기 위해서는 도출된 물성치가 해당 물질의 열분해 특성을 나타낼 수 있는지에 대한 검증이 필요하다.
본 연구에서는, 열분해 모델을 적용하여 단열재 화재를 해석하기 위해 열분해 특성을 결정하는 선행 연구로 단열재의 열분해 과정을 나타내는 열분해 특성인 열분해 물성치를 도출하고자 하였다. 여러 승온속도에 대하여 질소 조건에서 TGA 실험을 수행하여 열분해 특성을 얻었다. TGA 실험 결과로부터 model-free 법과 model-fitting 법을 동시에 적용하여 열분해 물성치, 반응 메커니즘을 결정하였다. 또한, 산출된 물성치를 FDS의 열분해 모델에 적용하여 TGA의 질량 감소 곡선과 시뮬레이션 결과를 비교하여 도출된 물성치의 적정성에 대하여 검토하였다.
2. 실험 방법 및 조건
2.1 시험 시편
단열재의 열분해 특성을 파악하기 위해 본 연구에 사용된 시편은 비드법 단열재(expanded polystyrene, EPS) 2종으로, 이는 회색 스티로폼으로 불린다. 흰색 스티로폼과 유사하지만, 내부에 첨가되어 있는 첨가제가 적외선 흡수체 및 반사체 역할을 함으로써 복사열의 영향을 상쇄시켜 흰색 스티로폼보다 향상된 단열성능을 보여준다. Figure 1은 K사에서 제작되고 있는 실험 시편 사진을, Table 1은 EPS의 열적 물성에 대해 나타내었다.
2.2 열중량 분석
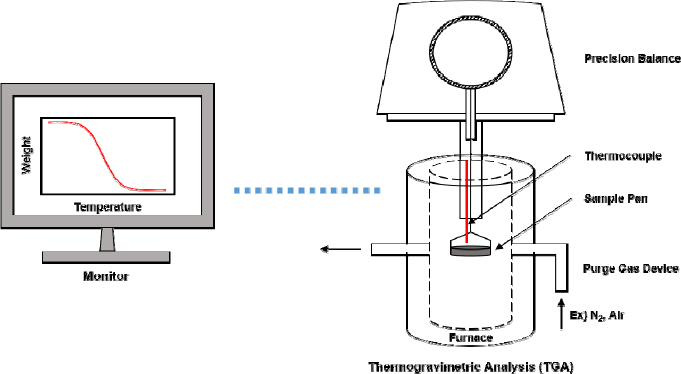
열중량 분석은 시간 또는 온도 변화에 따른 시편의 질량 변화를 측정하는 방법으로, Figure 2에 TGA 장치도를 나타내었다. TGA 실험으로부터 온도에 따른 질량 변화 곡선인 thermogravimetric (TG) 곡선과 이를 미분한 곡선인 derivative thermogravimetric (DTG) 곡선을 얻을 수 있는데, 이 곡선으로부터 열분해 온도 범위, 최대 반응 온도와 같은 열분해 특성을 결정할 수 있다.
본 연구에서는 EPS의 열분해 특성을 파악하기 위해 TA instruments 사에서 제작된 discovery TGA 55를 사용하여 TGA 실험을 수행하였다. TGA 실험에 사용된 EPS의 질량은 약 5 mg이며, 일정한 승온속도로 상온에서 800 ℃까지 가열시켰다. International Confederation for Thermal Analysis and Calorimetry에 따르면, TGA 실험 시 하나의 승온속도보다는 여러 승온속도(최소 3~5개)에 대해 결정된 열분해 특성이 더 정확하다고 알려진 바가 있으며(14), 이에 4개의 승온속도 조건(5, 10, 15, 20 ℃/min)을 적용하였다. 주입 가스는 열분해 반응만 고려하기 위해 연소반응에 참여하지 않는 불활성 기체인 질소를 사용하였다. 또한, 결과의 신뢰성 확보를 위해 총 3번의 실험을 수행하였으며, Table 2는 TGA 실험 조건을 정리하여 나타낸 것이다.
3. 반응속도 분석
3.1 반응속도
열분해 속도는 화재 성장 속도를 결정하므로 화재 거동을 예측하기 위해서는 정확한 열분해 속도가 필요하다. 열분해 속도를 예측하기 위해 열분석에서 사용되는 반응속도 모델은 식(1)과 같다(14).
여기서, α는 전환도(extent of conversion)로 식(2)와 같이 표현되며, k(T)는 반응 속도 상수로 식(3)과 같은 아레니우스 형태로 나타나고, f(α)는 반응 모델이다.
위 식에서, mi와 mf는 각각 초기, 최종 시편 무게를 mt는 반응 중 시간 t일 때 시편 무게를 의미하며, TGA 실험에서 얻을 수 있다.
여기서, T는 절대 온도(K), R는 일반기체상수(8.3143 J/mol⋅K), A와 E는 각각 선인자 계수와 활성화 에너지이다. 식(1)에 식(3)을 대입하면 아래 식(4)를 도출할 수 있으며, 식(4)는 고체 물질의 열분해 물성치를 결정하기 위해 반응속도 분석에 사용할 수 있다.
반응속도 분석에 많이 사용되는 방법으로는 model-free 법과 model-fitting 법이 있다. model-free 법은 고체 가연물의 반응 메커니즘에 의존하지 않고 활성화 에너지를 추정할 수 있지만, 반응 메커니즘이 고려되지 않아 선인자 계수를 도출하는 데에는 어려움이 있다. 반면, model-fitting 법은 반응 메커니즘에 따른 열분해 물성치를 결정할 수 있지만, 물질의 반응 메커니즘이 알려지지 않았다면 적절하게 도출하는 데에 어려움이 있다. 이러한 경우에는 model-free 법의 활성화 에너지와 model-fitting 법의 활성화 에너지를 비교하여 물질의 반응 메커니즘을 결정할 수 있다. 또한, model-free 법의 선인자 계수를 계산하기 위해 반응속도 보상효과를 적용할 수 있으며, 식(5)와 같이 표현된다(14).
여기서, Ai와 Ei는 각각 model-fitting 법을 통해 계산된 선인자 계수와 활성화 에너지이며, a와 b는 보상변수로 승온속도에 영향을 받는다. a와 b가 결정되고 나면, model-free 법의 활성화 에너지와 선인자 계수인 E0와 A0를 식(5)에 대입하고, 계산된 E0를 통해 A0를 결정할 수 있다.
본 연구에서는 model-free 법을 통해 EPS의 활성화 에너지를 도출하였다. 또한, 알려진 고체 상태 반응 메커니즘을 기반으로 model-fitting 법을 적용하여 계산된 활성화 에너지와 model-free 법의 활성화 에너지와 비교하였다. model-free 법과 비슷한 값을 나타내는 반응 메커니즘으로부터 선인자 계수를 계산하였다. 보상효과를 적용하여 보상변수를 결정하였고, 이를 바탕으로 model-free 법의 선인자 계수 A0를 도출하였다.
3.2 Model-free 법
물질의 활성화 에너지를 결정하는 데 있어 다양한 방법이 있으며 어떠한 방법으로 분석하는지에 따라 정량적인 차이가 발생할 수 있다(15-17). 본 연구에서는 model-free 법 중 Kissinger method, Flynn-Wall-Ozawa (FWO) method와 Starink method를 사용하여 활성화 에너지를 추정하였고 분석 방법에 따른 활성화 에너지 값을 정량적으로 비교하였다. Kissinger(18) 및 Blaine와 Kissinger(19)는 다양한 승온속도(β)에서 열분해 반응에 대해 일정한 활성화 에너지(Ea)를 도출하는 방법을 제안하였고, 식(4)를 기반으로 하여 온도 적분에 대한 근사를 통해 식(6)을 나타내었다.
여기서, Tp는 열분해 반응이 최대 속도로 일어나는 온도를 의미하며, 이 때 Ea는 ln(β/Tp2)와 1/Tp의 그래프를 나타내어 기울기로부터 계산할 수 있다. Kissinger와 달리 Ozawa(20), Flynn와 Wall(21) 및 Starink(22)는 여러 승온속도에서 열분해 반응의 전환도에 따른 온도에서 Ea를 추정하도록 제안하였으며, 근사 적분을 바탕으로 각각 식(7)과 식(8)으로 표현된다.
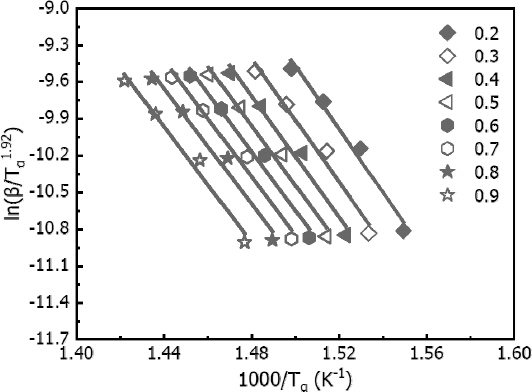
여기서, g(α)는 전환도의 적분 함수이고, Tα는 전환도에 따른 절대 온도(K)이다. FWO method의 경우에는 ln(β)와 1/Tα을 도시하고 직선으로부터, Starink method의 경우에는 ln(β/Tα1.92)와 1/Tα의 선형적인 관계로부터 전환도에 따른 Ea를 추정할 수 있다.
3.3 Model-fitting 법
본 연구에서는 EPS의 Ei와 Ai를 결정하기 위해 model -fitting 분석에서 흔히 사용되고 있는 방법 중 하나인 Coats -Redfern (CR) method을 선택하였으며, 식(9)과 같다(23).
전환도의 적분 함수 g(α)는 Table 3에 반응속도 분석 시 사용되는 고체상 반응 모델 일부를 정리하여 나타내었다(24). 이때 ln[g(α)/T2]와 1/T의 그래프 기울기인 -Ea/R로부터 Ea를, y 절편인 ln(AR/βEa)로부터 A를 계산할 수 있다.
4. 결과 및 분석
4.1 TGA 결과
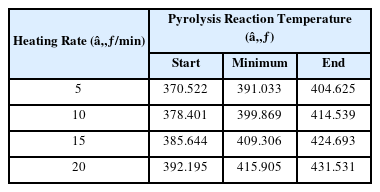
Figure 3은 질소 조건에서 4가지의 승온속도에 대한 EPS의 TGA 실험 결과로, 200-600 ℃의 온도 범위에서 질량감소량과 질량감소율에 대해 나타내었다. Figure 3(a)는 온도에 대한 질량을 나타내는 TG 곡선, Figure 3(b)는 온도에 대한 질량 감소를 보여주는 DTG 곡선이다. Figure 3(b)에서 DTG 곡선의 최소점에 해당하는 온도는 열분해의 최대 반응속도가 나타나는 온도이다. 최대 반응 온도를 기준으로 ISO 11358-1(25)을 적용하여 열분해 과정이 시작하고 종료되는 온도를 구할 수 있다. Table 4에 열분해 시작 및 종료 온도와 최대 반응 온도를 정리하였다. Figures 3(a)와 3(b)에서 승온속도가 증가함에 따라 그래프가 오른쪽으로 치우치는 경향이 보인다. 이는 승온속도가 증가하면 열분해 과정이 더 높은 온도에서 일어나는 것을 의미하며, Table 4를 통해서도 확인할 수 있다. 승온속도가 증가할수록 표면에 열이 가해지는 시간이 짧아져 열전달이 잘 이루어지지 않기 때문에, 열분해 온도가 상승한다(15,26,27). Table 5는 열분해가 시작되고 종료되는 온도에서의 질량을 나타낸 것이다. EPS는 열분해를 겪는 동안 약 70%의 질량이 감소하였으며, 승온속도는 질량 감소량에는 영향을 미치지 않는다. 승온속도의 변화는 시간당 전달되는 에너지의 양이 달라지는 것으로, 열분해 온도에 도달하는 시간의 차이를 주는 것이다. 질량 감소는 열분해 온도에 도달하면 EPS를 구성하는 성분이 동일하게 분해되기 때문에 승온속도 변화에 영향을 받지 않는 것으로 판단된다. Figure 3(b)를 보면, 모든 승온속도에 대해 DTG 곡선의 최소점이 하나만 존재하는데, 이는 EPS의 열분해가 한 번의 반응을 거쳐 일어난다는 것을 의미한다(10,11). 이에 EPS의 반응속도 분석 시 단일단계 과정으로 고려하여 해석하였다.
4.2 Model-free 법의 활성화 에너지
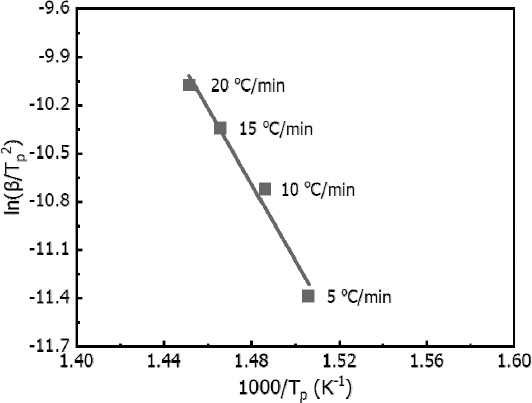
본 연구에서 EPS의 활성화 에너지를 산출하기 위해 TGA 실험으로부터 3가지 model-free 법을 적용하였으며, 분석법에 따른 정량적 차이를 검토하였다. Kissinger method의 경우, 전환도에 상관없이 전체 열분해 과정에 대해 일정한 활성화 에너지 값을 제공한다. Table 4에 제시되어 있는 각 승온속도(β)에서의 최대 반응 온도 값을 식(6)의 Tp에 대입하여 도시하였으며, 결과는 Figure 4와 같다. Figure 4에서 1차 함수로 표현된 직선의 기울기는 식(6)의 –Ea/R와 같으며 이로부터 활성화 에너지를 도출할 수 있다. Kissinger method를 바탕으로 계산된 EPS의 활성화 에너지 값은 196.3 kJ/mol이며, 이때 상관계수(R2)는 0.9758을 가진다.
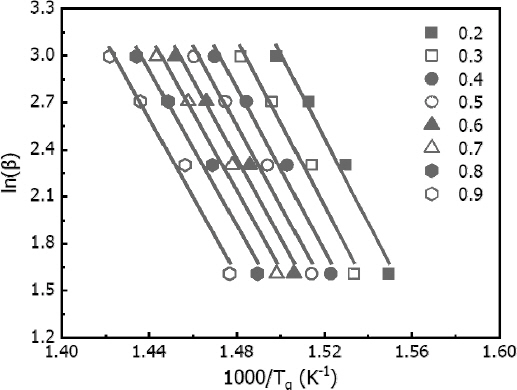
앞에서 제시된 Kissinger method와 달리, FWO method 및 Starink method는 열분해 과정의 전환도를 고려할 수 있어 반응 과정에 대한 활성화 에너지 값의 변화를 나타낼 수 있다. 본 연구에서는 전환도 0.2~0.9에 대해 0.1 간격으로 활성화 에너지를 계산하였다. Figures 5와 6은 각각 FWO method와 Starink method를 사용하여 각 승온속도에서 전환도에 따라 나타낸 것이며, 이때 Tα는 TGA 실험 결과인 Figure 3(a)로부터 측정되었다. 전환도에 대해 선형적인 관계를 확인하였으며, FWO method에서는 –1.0518Ea/R의 기울기로, Starink method는 –1.0008Ea/R의 기울기로부터 활성화 에너지를 산출하였다. 전환도 0.2-0.9에 대한 활성화 에너지 산출 시 상관계수(R2) 범위는 FWO method에서 0.97-0.9727, Starink method에서 0.9671-0.9698로 나타났다.
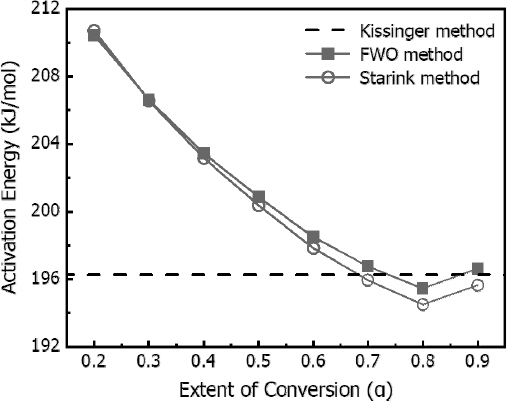
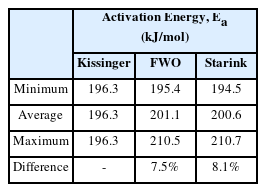
Figure 7은 3가지 model-free 법으로부터 계산한 각 전환도에서의 활성화 에너지를 나타낸 것으로, Kissinger method는 전환도를 고려하지 않으므로 점선으로 표시하였다. FWO method와 Starink method는 전환도에 따른 활성화 에너지 값의 경향이 유사하게 나타나는 것을 볼 수 있다. 최대 활성화 에너지 값은 각각 210.5 kJ/mol, 210.7 kJ/mol로 전환도가 0.2인 열분해 과정 초기에 나타났으며, Kissinger method와 비교하면 각각 7.2%, 7.3%의 차이를 보였다. 최소 활성화 에너지 값의 경우에는 각각 195.4 kJ/mol, 194.5 kJ/mol로 전환도가 0.8인 반응이 끝날 무렵에 나타났고, Kissinger method에서 계산된 값과 0.5%, 0.9% 차이가 난다. 전환도가 0.7인 경우 FWO method는 196.8 kJ/mol, Starink method는 195.9 kJ/mol로 Kissinger method의 활성화 에너지와 가장 유사한 값을 산출하였다. Table 6에는 전환도에서의 활성화 에너지가 최대⋅최소인 경우의 값과 모든 전환도에 대한 평균 활성화 에너지 값을 나타냈고, 최대⋅최소값과 평균값 사이의 편차를 구하였다. 최대⋅최소 활성화 에너지 값과 평균값 사이의 편차가 20-30% 미만일 때, 활성화 에너지가 전환도에 영향을 받지 않는다고 알려져 있다(7,10). FWO method와 Starink method의 편차는 각각 7.5%, 8.1%이기 때문에 평균값 201.1 kJ/mol, 200.6 kJ/mol을 각 방법의 대표하는 활성화 에너지로 결정하였다. Kissinger method를 통해 계산된 196.3 kJ/mol와 비교한다면, FWO method의 경우에는 약 2.4%, Starink method의 경우에는 약 2.2%로 큰 차이가 나지 않았다. 이에 EPS의 반응 메커니즘을 결정할 때 3가지 방법에서 결정된 대표 활성화 에너지 값을 평균한 199.3 kJ/mol을 기준값으로 적용하였다.
4.3 Coats-Redfern method를 통한 열분해 반응 메커니즘
본 연구에서 EPS의 반응 메커니즘을 결정하기 위해 CR method를 사용하였다. CR method는 model-free 법과 달리 하나의 승온속도에 대하여 각각의 활성화 에너지를 결정할 수 있다. 먼저, 식(9)으로부터 활성화 에너지를 계산하기 위해 g(α)는 3.3절의 Table 3에 제시된 모든 함수 g(α)에 대해 적용하였다. y축에 ln[g(α)/T2]를, x축에 1000/T를 도시하여 나타나는 기울기는 –Ea/R과 같기 때문에 이로부터 Ea를 구할 수 있다. Table 7에 하나의 승온속도에서 계산된 각 메커니즘의 Ea와 상관계수를 정리하여 나타내었다. 모든 메커니즘에서 높은 상관계수가 나타났지만, 열분해 반응 메커니즘에 따라 활성화 에너지 값이 크게 달라지는 것을 확인할 수 있으며, 이에 열분해 반응 메커니즘을 고려하는 것이 중요하다.
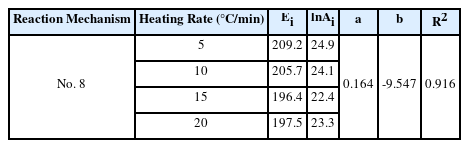
열분해 반응 메커니즘은 model-free 법의 활성화 에너지와 비교를 통해 결정할 수 있다. 앞서 model-free 법을 통해 결정된 활성화 에너지는 199.3 kJ/mol이며, 이를 model-fitting 법의 활성화 에너지와 비교하였다. 여러 메커니즘 중에서, No. 8에 해당하는 반응 메커니즘이 승온속도가 5, 10, 15, 20 ℃/min일 때 각각 209.2, 205.7, 196.4, 197.5 kJ/mol로 약 5.0, 3.2, 1.5, 0.9%의 가장 작은 오차를 보였다. 이에 EPS의 열분해는 No. 8에 해당하는 g(α) = 1 - (1 - α)1/2의 반응 메커니즘으로 표현하는 것이 적절하다.
열분해 반응 메커니즘이 결정되고 나면, model-fitting 법에서 선인자 계수를 도출할 수 있다. 식(9)의 g(α) = 1 - (1 - α)1/2를 대입하고, 각 승온속도에 대해 ln[g(α)/T2]와 1000/T를 그래프로 나타내었을 때의 y 절편인 ln(AR/βEa)을 통해 선인자 계수를 구하였으며, 이를 Table 8에 정리하였다.
4.4 Model-free 법의 선인자 계수
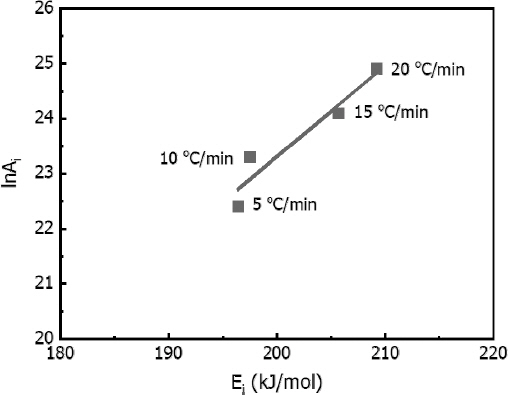
3장에서 언급했듯이, model-free 법의 선인자 계수는 보상효과를 통해 결정할 수 있다. 보상효과를 적용하기 위해 보상변수가 요구되며, 이는 승온속도에 영향을 받는다. Figure 8은 보상변수를 얻기 위해 각 승온속도에서 활성화 에너지(Ei)와 선인자 계수(Ai)의 관계를 선형적으로 나타낸 것으로 이를 통해 기울기인 a와 y 절편인 b가 결정된다. Table 9는 각 승온속도에 대해 Ei와 Ai로부터 결정된 보상변수와 상관계수를 나타낸 것이다. 이를 바탕으로 식(5)의 a와 b에 결정된 보상변수를 대입하고, lnAi와 Ei에 lnA0와 E0를 대입하면 식(10)을 얻을 수 있다. model-free 법의 활성화 에너지 값인 199.3 kJ/mol을 E0에 대입하여 model-free 법의 선인자 계수 A0 값 1.1E + 10 s-1를 도출하였다.
4.5 열분해 모델을 이용한 열분해 물성치 검토
본 연구에서는 화재 시뮬레이션인 FDS의 열분해 모델을 통해 도출된 물성치의 적정성을 검토하고자 한다. FDS의 열분해 모델 적용 시 입력 변수는 열 물성치인 밀도, 비열, 열전도도와 열분해 물성치인 활성화 에너지와 선인자 계수가 요구된다. EPS의 열 물성치는 Table 1에 제시된 값을, 열분해 물성치는 4가지 승온속도(5, 10, 15, 20 ℃/min)에 대해 반응속도 분석법에서 도출된 값을 사용하였다. FDS 열분해 모델에서 사용하는 반응속도(rαβ) 방정식은 식(11)과 같다(28,29).
여기서, 하첨자 α와 β는 각각 물질 성분과 반응 수이며, Aαβ는 선인자 계수, Ys,α는 성분 α의 초기 질량분율이고, ns,αβ는 반응차수, Eαβ는 활성화 에너지, Ts는 표면온도이다.
Figure 9(a)는 도출된 열분해 물성치를 적용한 반응속도 방정식 결과와 TGA 실험 결과를 비교하여 나타낸 것이다. 열분해 모델의 경우, 더 높은 온도에서 열분해가 일어나며 열분해 최대 반응 온도가 약 550 ℃로 실험보다 과대 예측하였으며 약 150 ℃ 차이가 난다. 열분해 모델에서 반응속도 수정을 위해 도출된 선인자 계수 값을 수정하여 보정하였다. Figure 9(b)는 보정된 선인자 계수 값을 적용한 반응속도 모델 결과와 10 ℃/min의 승온속도에 대한 TGA 실험 결과로, 실험 결과와 잘 일치하는 것을 확인하였다. 열분해 모델을 통해 EPS의 화재 해석을 수행하는 경우, 본 연구에서는 선인자 계수 값을 1.1E + 1013로 적용하여야 한다. 실험으로부터 도출된 열분해 물성치를 바로 사용한다면, 화재 현상을 과대⋅과소 예측할 가능성이 있다. 따라서 FDS 열분해 모델로 화재 현상을 구현하고자 할 때 실험과의 비교를 통해 검증이 반드시 필요하다.
5. 결 론
본 연구에서는 화재 시뮬레이션의 열분해 모델을 적용하여 EPS의 화재 현상을 구현하기 위한 선행연구로 EPS의 열분해 물성치, 반응 메커니즘을 얻고자 하였다. 4가지 승온속도에 대해 열중량 분석(TGA) 실험을 수행하여 열분해 특성이 검토되었다. EPS는 약 370-430 ℃의 온도 범위에서 한 번의 질량 감소를 통해 열분해가 일어나는 것을 확인했다. TGA 실험에서 얻은 열분해 특성으로부터 활성화 에너지, 선인자 계수와 반응 메커니즘을 결정하기 위해 여러 반응속도 분석법을 수행하였다.
Kissinger method를 통해 열분해 과정 동안 일정한 활성화 에너지를, Flynn-Wall-Ozawa (FWO)와 Starink method를 통해 전환도에 따른 활성화 에너지를 산출하였다. EPS의 활성화 에너지는 열분해 반응에서 전환도에 영향을 받지 않는 것을 확인했다. Kissinger, FWO, Starink method를 통해 산출된 열분해 반응의 활성화 에너지는 199.3 kJ/mol이다. 반응 메커니즘은 Coats-Redfern method를 통해 구했으며, g(α) = 1 - (1 - α)1/2의 함수로 열분해 반응을 적절하게 나타낼 수 있다. 선인자 계수는 보상효과를 적용하여 1.1E + 10 s-1 값을 얻었다. FDS의 열분해 모델을 통해 도출된 열분해 물성치의 적정성을 검토하였고, 화재 구현 시 선인자 계수 값이 1.1E + 13 s-1로 수정되어야 한다. 또한, 열분해 모델을 사용하기 전에 반드시 추정한 열분해 물성치에 대한 검증이 필요하다는 것을 제안하고자 한다.
후 기
이 논문은 부경대학교 자율창의학술연구비(2023년)에 의하여 연구되었음.